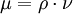Dynamic viscosity
From CFD-Wiki
(Difference between revisions)
| Line 1: | Line 1: | ||
| - | The SI unit of dynamic viscosity (Greek symbol: <math>\mu</math>) is | + | The SI unit of dynamic viscosity (Greek symbol: <math>\mu</math>) is pascal-second (<math>Pa\cdot s</math>), which is identical to <math>\frac{kg}{m\cdot s}</math>. |
The dynamic viscosity is related to the kinematic viscosity by | The dynamic viscosity is related to the kinematic viscosity by | ||
| - | + | :<math>\mu=\rho\cdot\nu</math> | |
| - | <math>\mu=\rho\cdot\nu</math | + | where <math>\rho</math> is the density and <math>\nu</math> is the [[kinematic viscosity]]. |
| - | + | ||
| - | where <math>\rho</math> is the | + | |
For the use in CFD, dynamic viscosity can be defined by different ways: | For the use in CFD, dynamic viscosity can be defined by different ways: | ||
* as a constant | * as a constant | ||
* as a function of temperature (e.g. piecewise-linear, piecewise-polynomial, polynomial, by [[Sutherland's law]] or by the [[Power-law viscosity law|Power law]]) | * as a function of temperature (e.g. piecewise-linear, piecewise-polynomial, polynomial, by [[Sutherland's law]] or by the [[Power-law viscosity law|Power law]]) | ||
| - | * by using | + | * by using Kinetic Theory |
* composition-dependent | * composition-dependent | ||
* by non-Newtonian models | * by non-Newtonian models | ||
{{stub}} | {{stub}} | ||
| - | |||
Latest revision as of 10:03, 12 June 2007
The SI unit of dynamic viscosity (Greek symbol: 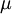 ) is pascal-second (
) is pascal-second (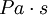 ), which is identical to
), which is identical to 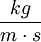 .
.
The dynamic viscosity is related to the kinematic viscosity by
where 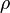 is the density and
is the density and 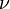 is the kinematic viscosity.
is the kinematic viscosity.
For the use in CFD, dynamic viscosity can be defined by different ways:
- as a constant
- as a function of temperature (e.g. piecewise-linear, piecewise-polynomial, polynomial, by Sutherland's law or by the Power law)
- by using Kinetic Theory
- composition-dependent
- by non-Newtonian models