Eddy viscosity ratio
From CFD-Wiki
m (fixed type and added stub marking) |
m (Reverted edits by DronrOlerr (Talk) to last version by Jola) |
||
| (6 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
| - | The eddy | + | The eddy viscosity ratio, <math>\frac{\mu_t}{\mu}</math>, is the ratio between the turbulent viscosity, <math>\mu_t</math>, and the molecular dynamic viscosity, <math>\mu</math>. |
| - | + | Eddy viscosity ratio is often also called turbulent viscosity ratio or simply viscosity ratio. | |
| + | |||
| + | ==Estimating the eddy viscosity ratio== | ||
| + | |||
| + | In order to obtain realistic inlet boundary conditions for the turbulence variables it is sometimes convenient to estimate the eddy viscosity ratio. The main advantage with using the eddy viscosity ratio is that this directly says something about how strong the influence of the turbulent viscosity is compared to the molecular viscosity. The eddy viscosity ratio is especially convenient to use in low-turbulence cases where it is difficult to guess any characteristic [[turbulent length scale]]. Typical examples are external aerodynamics, like flow around cars, aircrafts and submarines. For internal flows and flows where the origin of the turbulence can be related to some physical features of the problem it is often better to instead estimate the [[turbulent length scale]]. However, also when the turbulent length scale is used it is often good to double-check the resulting eddy viscosity ratio in order to make sure that the values are reasonable. | ||
[[Category:Dimensionless parameters]] | [[Category:Dimensionless parameters]] | ||
{{stub}} | {{stub}} | ||
Latest revision as of 12:26, 19 December 2008
The eddy viscosity ratio, 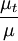 , is the ratio between the turbulent viscosity,
, is the ratio between the turbulent viscosity, 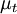 , and the molecular dynamic viscosity,
, and the molecular dynamic viscosity, 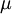 .
.
Eddy viscosity ratio is often also called turbulent viscosity ratio or simply viscosity ratio.
Estimating the eddy viscosity ratio
In order to obtain realistic inlet boundary conditions for the turbulence variables it is sometimes convenient to estimate the eddy viscosity ratio. The main advantage with using the eddy viscosity ratio is that this directly says something about how strong the influence of the turbulent viscosity is compared to the molecular viscosity. The eddy viscosity ratio is especially convenient to use in low-turbulence cases where it is difficult to guess any characteristic turbulent length scale. Typical examples are external aerodynamics, like flow around cars, aircrafts and submarines. For internal flows and flows where the origin of the turbulence can be related to some physical features of the problem it is often better to instead estimate the turbulent length scale. However, also when the turbulent length scale is used it is often good to double-check the resulting eddy viscosity ratio in order to make sure that the values are reasonable.
