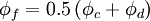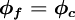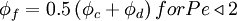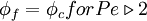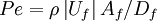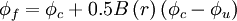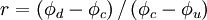Finite volume
From CFD-Wiki
Discretisation Schemes for convective terms in General Transport Equation. Finite-Volume Formulation, structured grids
Introduction
Here is describing the discretization schemes of the convective terms in the finite-volume equations. The accuracy, numerical stability and the boundness of the solution depends on the numerical scheme used for these terms. The central issue is the specification of an appropriate relationship between the convected variable, stored at the cell centre and its value at each of the cell faces.
Basic Equations of CFD
All the conservation equations can be written in the same generic differential form:
|
| (1) |
Equation (1) is integrated over a control volume and the following discretised equation for  is produced:
is produced:
|
| (2) |
whereis the source term for the control volume
, and
and
represent, respectively, the convective and diffusive fluxes of
across the control-volume face
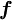
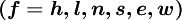
The convective fluxes through the cell faces are calculated as:
|
| (1) |
whereis the mass flow rate across the cell face
. The convected variable
associated with this mass flow rate is usually stored at the cell centres, and thus some form of interpolation assumption must be made in order to determine its value at each cell face. The interpolation procedure employed for this operation is the subject of the various schemes proposed in the literature and the accuracy, stability and boundedness of the solution depends on the procedure used.
In general, the value of 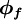 can be explicity formulated in terms of its neighbouring nodal values by a functional relationship of the form:
can be explicity formulated in terms of its neighbouring nodal values by a functional relationship of the form:
|
| (1) |
where 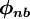 denotes the neighbouring-node
denotes the neighbouring-node 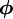 values.
Combining equations (\ref{eq3}) through (\ref{eq4a}), the discretised equation becomes:
values.
Combining equations (\ref{eq3}) through (\ref{eq4a}), the discretised equation becomes:
|
| (1) |
Convection Schemes
All the convection schemes involve a stencil of cells in which the values of 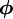 will be used to construct the face value
will be used to construct the face value 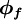
Where flow is from left to right, and 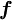 is the face in question.
is the face in question.
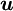 - mean Upstream node
- mean Upstream node
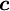 - mean Central node
- mean Central node
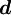 - mean Downstream node
- mean Downstream node
Basic Discretisation schemes
Central Differencing Scheme (CDS)
The most natural assumption for the cell-face value of the convected variable 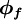 would appear to be the CDS, which calculates the cell-face value from:
would appear to be the CDS, which calculates the cell-face value from:
|
| (1) |
This scheme is 2nd-order accurate, but is unbounded so that unphysical oscillations appear in regions of strong convection and also in the presence of discontinuities such as shocks. The CDS may be used directly in very low Reynolds-number flows where diffusive effects dominate over convection.
Upwind Differencing Scheme (UDS)
The UDS assumes that the convected variable at the cell fase 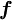 is the same as the upwind cell-centre value:
is the same as the upwind cell-centre value:
|
| (1) |
The UDS is unconditionally bounded and highly stable, but as noted earlier it is only 1st-order accurate in terms of truncation error and may produce severe numerical diffusion. The scheme is therefore highly diffusive when the flow direction is skewed relative to the grid lines.
Hybrid Differencing Scheme (HDS)
The HDS of Spalding [1972] switches the discretisation of the convection terms between CDS and UDS according to the local cell Peclet number as follows:
|
| (1) |
|
| (1) |
The cell Peclet number is defined as:
|
| (1) |
in which 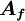 and
and 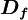 are respectively, the cell-face area and physical diffusion coefficient. When
are respectively, the cell-face area and physical diffusion coefficient. When 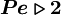 ,CDS calculations tends to become unstable so that theHDS reverts to the UDS. Physical diffusion is ignored when
,CDS calculations tends to become unstable so that theHDS reverts to the UDS. Physical diffusion is ignored when 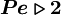 .
.
The HDS scheme is marginally more accurate than the UDS, because the 2nd-order CDS will be used in regions of low Peclet number.
High Resolution Schemes (HRS)
Classification of High Resolution Schemes
HRS can be classified as linear or non-linear, where linear means their coefficients are not direct functions of the convected variable when applied to a linear convection equation. It is important to recognise that linear convection schemes of 2nd-order accuracy or higher may suffer from unboudedness, and are not unconditionally stable.
Non-linear schemes analyse the solution within the stencil and adapt the discretisation to avoid any unwanted behavior, such as unboundedness (see Waterson [1994]). These two types of schemes may be presented in a unified way by use of the Flux-Limiter formulation (Waterson and Deconinck [1995]), which calculates the cell-face value of the convected variable from:
|
| (1) |
where $B \left( r \right)$ is termed a limiter function and the gradient ration $r$ is defined as:
|
| (1) |
The generalisation of this approach to handle non-uniform meshes has been given by Waterson [1994]
From equation (\ref{eq9}) it can be seen that $B=1$ gives the UDS and $B=r$ gives the CDS.
Numerical Implementation of HRS
The HRS schemes can be introdused into equation (\ref{eq4b}) by using the deffered correction procedure of Rubin and Khosla [1982]. This procedure express the cell-face value $\phi_{f}$ by:
\begin{equation}
\phi_{f}=\phi_{f}\left(U \right) + \phi^{'}_{f}
\label{eq10a}
\end{equation}
where $\phi^{'}_{f}$ is a higher-order correction which represents the difference between the UDS face value $\phi_{f}\left(U \right)$ and the higher-order scheme value $\phi_{f}\left(H \right)$, i.e.
\begin{equation}
\phi^{'}_{f}= \phi_{f}\left(H \right) + \phi_{f}\left(U \right)
\label{eq10b}
\end{equation}
If equation (\ref{eq10a}) is substituted into equation (\ref{eq4b}), the resulting discretised equation is:
\begin{equation}
\left\{ D_{h} + C_{h} \phi_{h} \left( U \right) \right\} - \left\{ D_{l} + C_{l} \phi_{l} \left( U \right) \right\} +
\left\{ D_{n} + C_{n} \phi_{n} \left( U \right) \right\} - \left\{ D_{s} + C_{s} \phi_{s} \left( U \right) \right\} +
\left\{ D_{e} + C_{e} \phi_{e} \left( U \right) \right\} - \left\{ D_{w} + C_{w} \phi_{w} \left( U \right) \right\} = S_{p} + B_{p}
\label{eq11}
\end{equation}
\\ . \\ where $B_{p}$ is the deferred-correction source terms, given by:
\begin{equation}
B_{p} = C_{l}\phi^{'}_{l} - C_{h}\phi^{'}_{h} +
C_{s}\phi^{'}_{s} - C_{n}\phi^{'}_{n} +
C_{w}\phi^{'}_{w} - C_{e}\phi^{'}_{e}
\label{eq12}
\end{equation}
This treatment leads to a diagonally dominant coefficient matrix since it is formed using the UDS.
The final form of the discretised equation:
\begin{equation}
a_{P}\phi_{P}= a_{N}\phi_{N} + a_{S}\phi_{S} +
a_{E}\phi_{E} + a_{W}\phi_{W} +
a_{H}\phi_{H} + a_{L}\phi_{L} + a_{T}\phi_{T} + S_{p} + B_{p}
\label{eq2}
\end{equation}
Subscrit $P$ represents the current computational cell; $N$, $S$, $E$, $W$, $H$, $L$ represent the six neighbouring cells and $T$ represents the previous timestep (transistent cases only)
The coefficients contain the appropriate contributions from the transient, convective and diffusive terms in (\ref{eq1})
Normalised Variables
Total Variation Diminishing (TVD)
Convection Boundedness Criterion (CBC)
Schemes
QUICK - Quadratic Upwind Interpolation for Convective Kinematics
LUS
Fromm
CUS

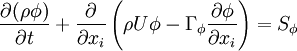
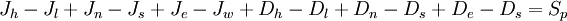
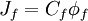
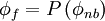
![\left\{ D_{h} + C_{h} \left[ P \left( \phi_{nb} \right) \right]_{h} \right\} -
\left\{ D_{l} + C_{l} \left[ P \left( \phi_{nb} \right) \right]_{l} \right\} +
\left\{ D_{n} + C_{n} \left[ P \left( \phi_{nb} \right) \right]_{n} \right\} -
\left\{ D_{s} + C_{s} \left[ P \left( \phi_{nb} \right) \right]_{s} \right\} +
\left\{ D_{e} + C_{e} \left[ P \left( \phi_{nb} \right) \right]_{e} \right\} -
\left\{ D_{w} + C_{w} \left[ P \left( \phi_{nb} \right) \right]_{w} \right\} = S_{p}](/W/images/math/8/a/7/8a710ce35af1c5c95cf741524ecd18f6.png)