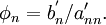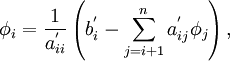Gaussian elimination
From CFD-Wiki
| Line 1: | Line 1: | ||
| - | == | + | == Description == |
We consider the system of linear equations '''<math> A\phi = B </math>''' or <br> | We consider the system of linear equations '''<math> A\phi = B </math>''' or <br> | ||
:<math> | :<math> | ||
| Line 97: | Line 97: | ||
where <math>i=n,n-1,\ldots,1</math>. | where <math>i=n,n-1,\ldots,1</math>. | ||
| + | |||
| + | == Algorithm == | ||
| + | Code or psuedo-code goes here. | ||
| + | |||
| + | == Important Considerations == | ||
| + | Gaussian elimination is best used for relatively small, relatively full systems of equations. If properly used, it will outperform iterative methods for these systems. However, it is important to keep in mind that the basic algorithm is vulnerable to accuracy issues. In practice, it is best to employ safeguards against such problems (e.g. pivoting). | ||
Revision as of 22:40, 16 December 2005
Description
We consider the system of linear equations 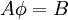 or
or
To perform Gaussian elimination starting with the above given system of equations we compose the augmented matrix equation in the form:
After performing elementary raw operations the augmented matrix is put into the upper triangular form:
The solution to the original system is found via back substitution. The solution to the last equation is
This result may now be substituted into the second to last equation, allowing us to solve for 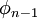 . Repetition of this substitution process will give us the complete solution vector. The back substitution process may be expressed as
. Repetition of this substitution process will give us the complete solution vector. The back substitution process may be expressed as
where 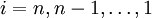 .
.
Algorithm
Code or psuedo-code goes here.
Important Considerations
Gaussian elimination is best used for relatively small, relatively full systems of equations. If properly used, it will outperform iterative methods for these systems. However, it is important to keep in mind that the basic algorithm is vulnerable to accuracy issues. In practice, it is best to employ safeguards against such problems (e.g. pivoting).

![\left[
\begin{matrix}
{a_{11} } & {a_{12} } & {...} & {a_{1n} } \\
{a_{21} } & {a_{22} } & . & {a_{21} } \\
. & . & . & . \\
{a_{n1} } & {a_{n1} } & . & {a_{nn} } \\
\end{matrix}
\right]
\left[
\begin{matrix}
{\phi_1 } \\
{\phi_2 } \\
. \\
{\phi_n } \\
\end{matrix}
\right]
=
\left[
\begin{matrix}
{b_1 } \\
{b_2 } \\
. \\
{b_n } \\
\end{matrix}
\right]](/W/images/math/a/4/d/a4dada28dd7a85c53604dc331829fc4e.png)
![\left[
\begin{matrix}
{a_{11} } & {a_{12} } & {...} & {a_{1n} } \\
{a_{21} } & {a_{22} } & . & {a_{21} } \\
. & . & . & . \\
{a_{n1} } & {a_{n1} } & . & {a_{nn} } \\
\end{matrix}
\left|
\begin{matrix}
{b_1 } \\
{b_2 } \\
. \\
{b_n } \\
\end{matrix}
\right.
\right]
\left[
\begin{matrix}
{\phi_1 } \\
{\phi_2 } \\
. \\
{\phi_n } \\
\end{matrix}
\right]](/W/images/math/4/7/e/47e9bee10079eb1421bd67e9bd451eaf.png)
![\left[
\begin{matrix}
{a_{11}^' } & {a_{12}^' } & {...} & {a_{1n}^' } \\
0 & {a_{22}^' } & . & {a_{2n}^' } \\
. & . & . & . \\
0 & 0 & . & {a_{nn}^' } \\
\end{matrix}
\left|
\begin{matrix}
{b_1^' } \\
{b_2^' } \\
. \\
{b_n^' } \\
\end{matrix}
\right.
\right]](/W/images/math/d/c/0/dc0b0d3482afa7d527b8f29f7fd72ea0.png)