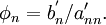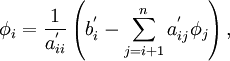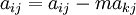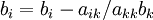Gaussian elimination
From CFD-Wiki
m (Gauss elimination moved to Gaussian elimination) |
(→Algorithm) |
||
| (18 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
| - | == | + | == Description == |
| - | We consider the system of linear equations '''<math> | + | We consider the system of linear equations '''<math> A\phi = b </math>''' or <br> |
:<math> | :<math> | ||
\left[ | \left[ | ||
| Line 12: | Line 12: | ||
\left[ | \left[ | ||
\begin{matrix} | \begin{matrix} | ||
| - | { | + | {\phi_1 } \\ |
| - | { | + | {\phi_2 } \\ |
. \\ | . \\ | ||
| - | { | + | {\phi_n } \\ |
\end{matrix} | \end{matrix} | ||
\right] | \right] | ||
| Line 52: | Line 52: | ||
\left[ | \left[ | ||
\begin{matrix} | \begin{matrix} | ||
| - | { | + | {\phi_1 } \\ |
| - | { | + | {\phi_2 } \\ |
. \\ | . \\ | ||
| - | { | + | {\phi_n } \\ |
\end{matrix} | \end{matrix} | ||
\right] | \right] | ||
</math> <br> | </math> <br> | ||
| - | After performing elementary | + | After performing elementary row operations the '''augmented matrix''' is put into the upper triangular form: <br> |
:<math> | :<math> | ||
| Line 74: | Line 74: | ||
\begin{matrix} | \begin{matrix} | ||
{b_1^' } \\ | {b_1^' } \\ | ||
| - | { | + | {b_2^' } \\ |
. \\ | . \\ | ||
| - | { | + | {b_n^' } \\ |
\end{matrix} | \end{matrix} | ||
| Line 84: | Line 84: | ||
</math> <br> | </math> <br> | ||
| - | + | The solution to the original system is found via '''back substitution'''. The solution to the last equation is | |
| + | |||
:<math> | :<math> | ||
| - | + | \phi_n = b_n^'/a_{nn}'. | |
| - | </math> <br> | + | </math> |
| - | + | ||
| + | This result may now be substituted into the second to last equation, allowing us to solve for <math>\phi_{n-1}</math>. Repetition of this substitution process will give us the complete solution vector. The back substitution process may be expressed as | ||
| + | |||
| + | :<math> | ||
| + | \phi_i = {1 \over {a_{ii}^' }}\left( {b_i^' - \sum\limits_{j = i + 1}^n {a_{ij}^' \phi_j } } \right), | ||
| + | </math> | ||
| + | |||
| + | where <math>i=n,n-1,\ldots,1</math>. | ||
| + | |||
| + | == Algorithm == | ||
| + | Forward elimination phase | ||
| + | : for k:= 1 step until n-1 do <br> | ||
| + | :: for i:=k+1 step until n do <br> | ||
| + | ::: <math>m = {{a_{ik} } \over {a_{kk} }} </math> <br> | ||
| + | ::: for j:= 1 step until n do <br> | ||
| + | :::: <math> a_{ij}=a_{ij}-ma_{kj}</math> <br> | ||
| + | ::: end loop (j) <br> | ||
| + | ::: <math>b_i=b_i-mb_k</math> <br> | ||
| + | :: end loop (i) <br> | ||
| + | : end loop (k) <br> | ||
| + | Back substitution phase | ||
| + | : for k:= n stepdown until 1 do <br> | ||
| + | :: for i:= 1 step until k-1 do <br> | ||
| + | ::: <math>b_i=b_i-a_{ik}/a_{kk}b_{k}</math> <br> | ||
| + | :: end loop (i) <br> | ||
| + | :: <math>\phi_{k}=b_{k}/a_{kk}</math><br> | ||
| + | : end loop (k) | ||
| + | == Important Considerations == | ||
| + | Gaussian elimination is best used for relatively small, relatively full systems of equations. If properly used, it should outperform most iterative methods for these systems. As the system to be solved becomes larger, the overhead associated with the more complicated iterative methods becomes less of an issue, and the iterative methods should outperform Gaussian Elimination. For sparse systems, the use of Gaussian elimination is complicated by the possible introduction of more nonzero entries (fill-in). In any case, it is important to keep in mind that the basic algorithm is vulnerable to accuracy issues, including (but not limited to) the distinct possibility of division by zero at various places in the solution process. In practice, it is best to employ safeguards against such problems (e.g. pivoting). | ||
| - | + | ==External link== | |
| - | + | *[http://en.wikipedia.org/wiki/Gaussian_elimination Wikipedia's article ''Gaussian elimination''] | |
Latest revision as of 15:08, 22 August 2007
Contents |
Description
We consider the system of linear equations 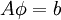 or
or
To perform Gaussian elimination starting with the above given system of equations we compose the augmented matrix equation in the form:
After performing elementary row operations the augmented matrix is put into the upper triangular form:
The solution to the original system is found via back substitution. The solution to the last equation is
This result may now be substituted into the second to last equation, allowing us to solve for 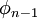 . Repetition of this substitution process will give us the complete solution vector. The back substitution process may be expressed as
. Repetition of this substitution process will give us the complete solution vector. The back substitution process may be expressed as
where 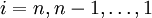 .
.
Algorithm
Forward elimination phase
- for k:= 1 step until n-1 do
- for i:=k+1 step until n do
-
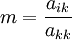
- for j:= 1 step until n do
-
- end loop (j)
-
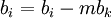
-
- end loop (i)
- for i:=k+1 step until n do
- end loop (k)
Back substitution phase
- for k:= n stepdown until 1 do
- for i:= 1 step until k-1 do
-
- end loop (i)
-
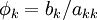
- for i:= 1 step until k-1 do
- end loop (k)
Important Considerations
Gaussian elimination is best used for relatively small, relatively full systems of equations. If properly used, it should outperform most iterative methods for these systems. As the system to be solved becomes larger, the overhead associated with the more complicated iterative methods becomes less of an issue, and the iterative methods should outperform Gaussian Elimination. For sparse systems, the use of Gaussian elimination is complicated by the possible introduction of more nonzero entries (fill-in). In any case, it is important to keep in mind that the basic algorithm is vulnerable to accuracy issues, including (but not limited to) the distinct possibility of division by zero at various places in the solution process. In practice, it is best to employ safeguards against such problems (e.g. pivoting).

![\left[
\begin{matrix}
{a_{11} } & {a_{12} } & {...} & {a_{1n} } \\
{a_{21} } & {a_{22} } & . & {a_{21} } \\
. & . & . & . \\
{a_{n1} } & {a_{n1} } & . & {a_{nn} } \\
\end{matrix}
\right]
\left[
\begin{matrix}
{\phi_1 } \\
{\phi_2 } \\
. \\
{\phi_n } \\
\end{matrix}
\right]
=
\left[
\begin{matrix}
{b_1 } \\
{b_2 } \\
. \\
{b_n } \\
\end{matrix}
\right]](/W/images/math/a/4/d/a4dada28dd7a85c53604dc331829fc4e.png)
![\left[
\begin{matrix}
{a_{11} } & {a_{12} } & {...} & {a_{1n} } \\
{a_{21} } & {a_{22} } & . & {a_{21} } \\
. & . & . & . \\
{a_{n1} } & {a_{n1} } & . & {a_{nn} } \\
\end{matrix}
\left|
\begin{matrix}
{b_1 } \\
{b_2 } \\
. \\
{b_n } \\
\end{matrix}
\right.
\right]
\left[
\begin{matrix}
{\phi_1 } \\
{\phi_2 } \\
. \\
{\phi_n } \\
\end{matrix}
\right]](/W/images/math/4/7/e/47e9bee10079eb1421bd67e9bd451eaf.png)
![\left[
\begin{matrix}
{a_{11}^' } & {a_{12}^' } & {...} & {a_{1n}^' } \\
0 & {a_{22}^' } & . & {a_{2n}^' } \\
. & . & . & . \\
0 & 0 & . & {a_{nn}^' } \\
\end{matrix}
\left|
\begin{matrix}
{b_1^' } \\
{b_2^' } \\
. \\
{b_n^' } \\
\end{matrix}
\right.
\right]](/W/images/math/d/c/0/dc0b0d3482afa7d527b8f29f7fd72ea0.png)