Gradient-based methods
From CFD-Wiki
Shenren CN (Talk | contribs) |
Shenren CN (Talk | contribs) |
||
| Line 7: | Line 7: | ||
where <math>U</math> and <math>\alpha</math> are the flow variable vector and the design variable vector respectively. <math>U</math> and <math>\alpha</math> are implicitly related through the flow equation, which is represented by a residual function driven to zero. | where <math>U</math> and <math>\alpha</math> are the flow variable vector and the design variable vector respectively. <math>U</math> and <math>\alpha</math> are implicitly related through the flow equation, which is represented by a residual function driven to zero. | ||
| - | <math> | + | <math>{R}(U(\alpha),\alpha)=0</math> |
Finite difference method: | Finite difference method: | ||
Revision as of 03:12, 24 January 2011
As its name means, gradient-based methods need the gradient of objective functions to design variables. The evaluation of gradient can be achieved by finite difference method, linearized method or adjoint method. Both finite difference method and linearized method has a time-cost proportional to the number of design variables and not suitable for design optimization with a large number of design variables. Apart from that, finite difference method has a notorious disadvantage of subtraction cancellation and is not recommended for practical design application.
Suppose a cost function 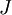 is defined as follows,
is defined as follows,
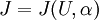
where 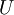 and
and 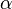 are the flow variable vector and the design variable vector respectively.
are the flow variable vector and the design variable vector respectively. 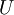 and
and 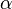 are implicitly related through the flow equation, which is represented by a residual function driven to zero.
are implicitly related through the flow equation, which is represented by a residual function driven to zero.
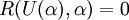
Finite difference method:
Linearized method:
Adjoint method:
