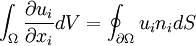Greens theorem
From CFD-Wiki
(Difference between revisions)
m |
|||
| (One intermediate revision not shown) | |||
| Line 1: | Line 1: | ||
''Greens Theorem'', also known as ''Divergence Theorem'' is an important identity in vector calculus. If <math>u_i</math> is a vector field variable defined over a domain <math>\Omega</math> then Greens Theorem states that | ''Greens Theorem'', also known as ''Divergence Theorem'' is an important identity in vector calculus. If <math>u_i</math> is a vector field variable defined over a domain <math>\Omega</math> then Greens Theorem states that | ||
| - | <math> | + | :<math> |
\int_\Omega \frac{\partial u_i}{\partial x_i} dV = \oint_{\partial \Omega} u_i n_i dS | \int_\Omega \frac{\partial u_i}{\partial x_i} dV = \oint_{\partial \Omega} u_i n_i dS | ||
</math> | </math> | ||
where <math>\partial\Omega</math> represents the boundary of <math>\Omega</math> and <math>n_i</math> is the unit outward normal to <math>\partial\Omega</math>. | where <math>\partial\Omega</math> represents the boundary of <math>\Omega</math> and <math>n_i</math> is the unit outward normal to <math>\partial\Omega</math>. | ||
Latest revision as of 11:40, 12 September 2005
Greens Theorem, also known as Divergence Theorem is an important identity in vector calculus. If 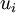 is a vector field variable defined over a domain
is a vector field variable defined over a domain 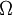 then Greens Theorem states that
then Greens Theorem states that
where 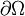 represents the boundary of
represents the boundary of 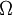 and
and 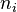 is the unit outward normal to
is the unit outward normal to 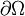 .
.