Heat transfer
From CFD-Wiki
(Difference between revisions)
| Line 4: | Line 4: | ||
*Mathematically, it can be described by using the Fourier's law: | *Mathematically, it can be described by using the Fourier's law: | ||
| - | :<math> | + | :<math>Q_{Conduction} = -k*A*\frac{dT}{dx}</math> |
| - | + | ||
| - | </math> | + | |
Where | Where | ||
| - | + | :<math>Q = \mbox{Heat conducted}\;[W]</math> | |
| - | + | :<math>k = \mbox{Thermal conductivity of the material}\;[W/m\,K]</math> | |
| - | + | :<math>A = \mbox{Cross-sectional area of the object parallel to heat conduction}\;[m^2]</math> | |
| - | + | :<math>T = \mbox{Temperature}\;[K]</math> | |
| - | + | :<math>x = \mbox{Length of the object}\;[m]</math> | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
== Convection == | == Convection == | ||
Revision as of 12:40, 1 December 2005
== Conduction ==
- Conduction can be defined as the heat transfer through a substance because of a temperature gradient. The rate of heat transfer by conduction between two regions of a substance is proportional to the temperature difference between them. The constant of propotionality is called thermal conductivity of the material.
- Mathematically, it can be described by using the Fourier's law:
Where

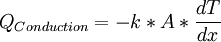
![Q = \mbox{Heat conducted}\;[W]](/W/images/math/c/e/5/ce5124f80c7625563c71a92efbe7c2a6.png)
![k = \mbox{Thermal conductivity of the material}\;[W/m\,K]](/W/images/math/1/f/4/1f4bf7ced6f34761ea9094f175e69505.png)
![A = \mbox{Cross-sectional area of the object parallel to heat conduction}\;[m^2]](/W/images/math/e/2/f/e2f59ce86b4e5a3439047c0b694eeab4.png)
![T = \mbox{Temperature}\;[K]](/W/images/math/2/3/c/23cda486a79eec21f05397bb3942be3e.png)
![x = \mbox{Length of the object}\;[m]](/W/images/math/5/9/a/59a8c70d997eb066da1c3eef42a80b56.png)