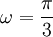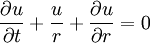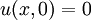ICASE/LaRC workshop on benchmark problems in computational aeroacoustics, category 1, problem 2
From CFD-Wiki
(Difference between revisions)
m (ICASE/LaRC Workshop on Benchmark Problems in Computational Aeroacoustics, Category 1, Problem 2 moved to ICASE/LaRC workshop on benchmark problems in computational aeroacoustics, category 1, problem 2) |
|||
| (4 intermediate revisions not shown) | |||
| Line 5: | Line 5: | ||
| - | Computer the Numerical solution at t=100,200,300 and 400.Use a domain of [5,450].The boundary condition at r=5 is u(5,t)= sin( | + | Computer the Numerical solution at t=100,200,300 and 400.Use a domain of [5,450].The boundary condition at r=5 is u(5,t)= sin(<math>\omega </math> t ).Perform computation for |
| - | a) | + | a) <math>\omega =\frac{\pi}{4}</math> |
| - | b) | + | b) <math>\omega =\frac{\pi}{3}</math> |
== Exact Solution == | == Exact Solution == | ||
| - | + | ||
== Comparison == | == Comparison == | ||
Latest revision as of 21:07, 18 February 2007
Solve the initial value problem
Computer the Numerical solution at t=100,200,300 and 400.Use a domain of [5,450].The boundary condition at r=5 is u(5,t)= sin(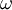
t ).Perform computation for
a) 
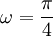b) 
