Introduction to turbulence/Statistical analysis/Estimation from a finite number of realizations
From CFD-Wiki
(Difference between revisions)
(→Bias and convergence of estimators) |
(→Bias and convergence of estimators) |
||
| Line 12: | Line 12: | ||
A procedure for answering these questions will be illustrated by considerind a simple '''estimator''' for the mean, the arithmetic mean considered above, <math>X_{N}</math>. For <math>N</math> independent realizations <math>x_{n}, n=1,2,...,N</math> where <math>N</math> is finite, <math>X_{N}</math> is given by: | A procedure for answering these questions will be illustrated by considerind a simple '''estimator''' for the mean, the arithmetic mean considered above, <math>X_{N}</math>. For <math>N</math> independent realizations <math>x_{n}, n=1,2,...,N</math> where <math>N</math> is finite, <math>X_{N}</math> is given by: | ||
| + | |||
| + | <table width="100%"><tr><td> | ||
| + | :<math> | ||
| + | fdsgfdsg | ||
| + | </math> | ||
| + | </td><td width="5%">(2)</td></tr></table> | ||
Revision as of 06:50, 7 June 2006
Estimators for averaged quantities
Since there can never an infinite number of realizations from which ensemble averages (and probability densities) can be computed, it is essential to ask: How many realizations are enough? The answer to this question must be sought by looking at the statistical properties of estimators based on a finite number of realization. There are two questions which must be answered. The first one is:
- Is the expected value (or mean value) of the estimator equal to the true ensemble mean? Or in other words, is yje estimator unbiased?
The second question is
- Does the difference between the and that of the true mean decrease as the number of realizations increases? Or in other words, does the estimator converge in a statistical sense (or converge in probability). Figure 2.9 illustrates the problems which can arise.
Bias and convergence of estimators
A procedure for answering these questions will be illustrated by considerind a simple estimator for the mean, the arithmetic mean considered above, 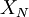 . For
. For 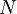 independent realizations
independent realizations 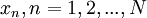 where
where 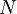 is finite,
is finite, 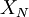 is given by:
is given by:
|
| (2) |