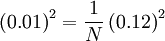Introduction to turbulence/Statistical analysis/Estimation from a finite number of realizations
From CFD-Wiki
(→Bias and convergence of estimators) |
m (Estimation from a Finite Number of Realizations moved to Estimation from a finite number of realizations: Correct case in title) |
Revision as of 11:35, 18 June 2007
Estimators for averaged quantities
Since there can never an infinite number of realizations from which ensemble averages (and probability densities) can be computed, it is essential to ask: How many realizations are enough? The answer to this question must be sought by looking at the statistical properties of estimators based on a finite number of realization. There are two questions which must be answered. The first one is:
- Is the expected value (or mean value) of the estimator equal to the true ensemble mean? Or in other words, is yje estimator unbiased?
The second question is
- Does the difference between the and that of the true mean decrease as the number of realizations increases? Or in other words, does the estimator converge in a statistical sense (or converge in probability). Figure 2.9 illustrates the problems which can arise.
Bias and convergence of estimators
A procedure for answering these questions will be illustrated by considerind a simple estimator for the mean, the arithmetic mean considered above, 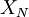 . For
. For 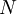 independent realizations
independent realizations 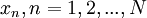 where
where 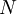 is finite,
is finite, 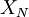 is given by:
is given by:
|
| (2) |
Now, as we observed in our simple coin-flipping experiment, since the 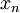 are random, so must be the value of the estimator
are random, so must be the value of the estimator 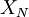 . For the estimator to be unbiased, the mean value of
. For the estimator to be unbiased, the mean value of 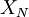 must be true ensemble mean,
must be true ensemble mean, 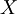 , i.e.
, i.e.
|
| (2) |
It is easy to see that since the operations of averaging adding commute,
|
| (2) |
(Note that the expected value of each 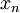 is just
is just 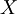 since the
since the 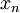 are assumed identically distributed). Thus
are assumed identically distributed). Thus 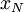 is, in fact, an unbiased estimator for the mean.
is, in fact, an unbiased estimator for the mean.
The question of convergence of the estimator can be addressed by defining the square of variability of the estimator, say 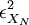 , to be:
, to be:
|
| (2) |
Now we want to examine what happens to 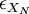 as the number of realizations increases. For the estimator to converge it is clear that
as the number of realizations increases. For the estimator to converge it is clear that 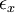 should decrease as the number of sample increases. Obviously, we need to examine the variance of
should decrease as the number of sample increases. Obviously, we need to examine the variance of 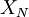 first. It is given by:
first. It is given by:
|
| (2) |
since 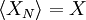 from equation 2.46. Using the fact that operations of averaging and summation commute, the squared summation can be expanded as follows:
from equation 2.46. Using the fact that operations of averaging and summation commute, the squared summation can be expanded as follows:
|
| (2) |
where the next to last step follows from the fact that the 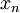 are assumed to be statistically independent samples (and hence uncorrelated), and the last step from the definition of the variance. It follows immediately by substitution into equation 2.49 that the square of the variability of the estimator,
are assumed to be statistically independent samples (and hence uncorrelated), and the last step from the definition of the variance. It follows immediately by substitution into equation 2.49 that the square of the variability of the estimator, 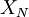 , is given by:
, is given by:
|
| (2) |
Thus the variability of the stimator depends inversely on the number of independent realizations, 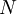 , and linearly on the relative fluctuation level of the random variable itself
, and linearly on the relative fluctuation level of the random variable itself 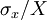 . Obviously if the relative fluctuation level is zero (either because there the quantity being measured is constant and there are no measurement errors), then a single measurement will suffice. On the other hand, as soon as there is any fluctuation in the
. Obviously if the relative fluctuation level is zero (either because there the quantity being measured is constant and there are no measurement errors), then a single measurement will suffice. On the other hand, as soon as there is any fluctuation in the 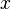 itself, the greater the fluctuation ( relative to the mean of
itself, the greater the fluctuation ( relative to the mean of 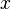 ,
, 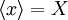 ), then the more independent samples it will take to achieve a specified accuracy.
), then the more independent samples it will take to achieve a specified accuracy.
Example: In a given ensemble the relative fluctuation level is 12% (i.e. 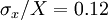 ). What is the fewest number of independent samples that must be acquired to measure the mean value to within 1%?
). What is the fewest number of independent samples that must be acquired to measure the mean value to within 1%?
AnswerUsing equation 2.52, and taking 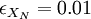 , it follows that:
, it follows that:
|
| (2) |
or 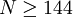 .
.

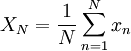
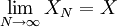
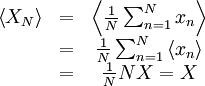
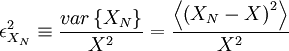
![\begin{matrix}
var \left\{ X_{N} \right\} & = & \left\langle X_{N} - X^{2} \right\rangle \\
& = & \left\langle \left[ \lim_{N\rightarrow\infty} \frac{1}{N} \sum^{N}_{n=1} \left( x_{n} - X \right) \right]^{2} \right\rangle - X^{2}\\
\end{matrix}](/W/images/math/4/2/a/42a377d205dfa9f0689df6d6bac1a092.png)
![\begin{matrix}
\left\langle \left[ \lim_{N\rightarrow\infty} \sum^{N}_{n=1} \left( x_{n} - X \right) \right]^{2} \right\rangle & = & \lim_{N\rightarrow\infty}\frac{1}{N^{2}} \sum^{N}_{n=1} \sum^{N}_{m=1} \left\langle \left( x_{n} - X \right) \left( x_{m} - X \right) \right\rangle \\
& = & \lim_{N\rightarrow\infty}\frac{1}{N^{2}}\sum^{N}_{n=1}\left\langle \left( x_{n} - X \right)^{2} \right\rangle \\
& = & \frac{1}{N} var \left\{ x \right\} \\
\end{matrix}](/W/images/math/a/0/9/a096bbb794633b599445da44489f9cb6.png)
![\begin{matrix}
\epsilon^{2}_{X_{N}}& =& \frac{1}{N}\frac{var\left\{x\right\}}{X^{2}} \\
& = & \frac{1}{N} \left[ \frac{\sigma_{x}}{X} \right]^{2} \\
\end{matrix}](/W/images/math/5/a/f/5af293e636864266f2d192289618d56e.png)