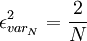Introduction to turbulence/Statistical analysis/Generalization to the estimator of any quantity
From CFD-Wiki
| (10 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
| + | {{Introduction to turbulence menu}} | ||
Similar relations can be formed for the estimator of any function of the random variable say <math>f(x)</math>. For example, an estimator for the average of <math>f</math> based on <math>N</math> realizations is given by: | Similar relations can be formed for the estimator of any function of the random variable say <math>f(x)</math>. For example, an estimator for the average of <math>f</math> based on <math>N</math> realizations is given by: | ||
| - | + | :<math>F_{N}\equiv\frac{1}{N}\sum^{N}_{n=1}f_{n}</math> | |
| - | :<math> | + | |
| - | F_{N}\equiv\frac{1}{N}\sum^{N}_{n=1}f_{n} | + | |
| - | </math> | + | |
| - | + | ||
where <math>f_{n}\equiv f(x_{n})</math>. It is straightforward to show that this estimator is unbiased, and its variability (squared) is given by: | where <math>f_{n}\equiv f(x_{n})</math>. It is straightforward to show that this estimator is unbiased, and its variability (squared) is given by: | ||
| - | + | :<math> | |
| - | :<math> | + | |
\epsilon^{2}_{F_{N}}= \frac{1}{N} \frac{var \left\{f \left( x \right) \right\}}{\left\langle f \left( x \right) \right\rangle^{2} } | \epsilon^{2}_{F_{N}}= \frac{1}{N} \frac{var \left\{f \left( x \right) \right\}}{\left\langle f \left( x \right) \right\rangle^{2} } | ||
</math> | </math> | ||
| - | |||
'''Example:''' Suppose it is desired to estimate the variability of an estimator for the variance based on a finite number of samples as: | '''Example:''' Suppose it is desired to estimate the variability of an estimator for the variance based on a finite number of samples as: | ||
| - | |||
:<math> | :<math> | ||
var_{N} \left\{x \right\} \equiv \frac{1}{N} \sum^{N}_{n=1} \left( x_{n} - X \right)^{2} | var_{N} \left\{x \right\} \equiv \frac{1}{N} \sum^{N}_{n=1} \left( x_{n} - X \right)^{2} | ||
</math> | </math> | ||
| - | |||
(Note that this estimator is not really very useful since it presumes that the mean value, <math>X</math>, is known, whereas in fact usually only <math>X_{N}</math> is obtainable). | (Note that this estimator is not really very useful since it presumes that the mean value, <math>X</math>, is known, whereas in fact usually only <math>X_{N}</math> is obtainable). | ||
| Line 27: | Line 20: | ||
'''Answer''' | '''Answer''' | ||
| - | Let <math>f=(x-X)^2</math> in equation 2 | + | Let <math>f=(x-X)^2</math> in equation the equation for <math>\epsilon^{2}_{F_{N}}</math> above so that <math>F_{N}= var_{N}\left\{ x \right\}</math>, <math>\left\langle f \right\rangle = var \left\{ x \right\} </math> and <math>var \left\{f \right\} = var \left\{ \left( x-X \right)^{2} - var \left[ x-X \right] \right\}</math>. Then: |
| + | |||
| + | :<math> | ||
| + | \epsilon^{2}_{F_{N}}= \frac{1}{N} \frac{var \left\{ \left( x-X \right)^{2} - var \left[x \right] \right\} }{ \left( var \left\{ x \right\} \right)^{2} } | ||
| + | </math> | ||
| + | |||
| + | This is easiest to understand if we first expand only the numerator to oblain: | ||
| + | |||
| + | :<math> | ||
| + | var \left\{ \left( x- X \right)^{2} - var\left[x \right] \right\} = \left\langle \left( x- X \right)^{4} \right\rangle - \left[ var \left\{ x \right\} \right]^2 | ||
| + | </math> | ||
| + | |||
| + | Thus | ||
| + | |||
| + | :<math> | ||
| + | \epsilon^{2}_{var_{N}} = \frac{\left\langle \left( x- X \right)^4 \right\rangle}{\left[ var \left\{ x \right\} \right]^2 } - 1 | ||
| + | </math> | ||
| + | |||
| + | Obviuosly to proceed further we need to know how the fourth central moment relates to the second central moment. As noted earlier, in general thi is ''not'' known. If, however, it is reasonable to assume that <math>x</math> is a Gaussian distributed random variable, we know from the previous section on [[Probability in turbulence#Skewness and kurtosis|skewness and kurtosis]] that the kirtosis is 3. Then for Gaussian distributed random variables, | ||
| + | |||
| + | :<math> | ||
| + | \epsilon^{2}_{var_{N}} = \frac{2}{N} | ||
| + | </math> | ||
| + | |||
| + | Thus the number of independnt data required to produce the same level of convergence for an estimate of the variance of a Gaussian distributed random variable is <math>\sqrt{2}</math> times that of mean, It is easy to show that the higher the moment, the more the amount of data required. | ||
| + | |||
| + | As noted earlier, turbulence problems are not usually Gaussian, and in fact values of the kurtosis substantionally greater than 3 are commonly encountered, especially for the moments of differentiated quantities. Clearly the non-Gaussian nature of random variables can affect the planning of experiments, since substantially greater amounts of data can be required to achieved the necessary statistical accuracy. | ||
| + | |||
| + | {{Turbulence credit wkgeorge}} | ||
| + | |||
| + | {{Chapter navigation|Estimation from a finite number of realizations}} | ||
Latest revision as of 17:30, 25 June 2007
Similar relations can be formed for the estimator of any function of the random variable say 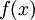 . For example, an estimator for the average of
. For example, an estimator for the average of 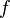 based on
based on 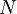 realizations is given by:
realizations is given by:
where 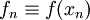 . It is straightforward to show that this estimator is unbiased, and its variability (squared) is given by:
. It is straightforward to show that this estimator is unbiased, and its variability (squared) is given by:
Example: Suppose it is desired to estimate the variability of an estimator for the variance based on a finite number of samples as:
(Note that this estimator is not really very useful since it presumes that the mean value, 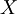 , is known, whereas in fact usually only
, is known, whereas in fact usually only 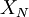 is obtainable).
is obtainable).
Answer
Let 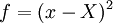 in equation the equation for
in equation the equation for 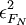 above so that
above so that 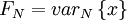 ,
, 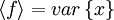 and
and ![var \left\{f \right\} = var \left\{ \left( x-X \right)^{2} - var \left[ x-X \right] \right\}](/W/images/math/4/9/0/490a881ef051ed37db7bccb8888989bf.png) . Then:
. Then:
This is easiest to understand if we first expand only the numerator to oblain:
Thus
Obviuosly to proceed further we need to know how the fourth central moment relates to the second central moment. As noted earlier, in general thi is not known. If, however, it is reasonable to assume that 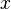 is a Gaussian distributed random variable, we know from the previous section on skewness and kurtosis that the kirtosis is 3. Then for Gaussian distributed random variables,
is a Gaussian distributed random variable, we know from the previous section on skewness and kurtosis that the kirtosis is 3. Then for Gaussian distributed random variables,
Thus the number of independnt data required to produce the same level of convergence for an estimate of the variance of a Gaussian distributed random variable is 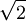 times that of mean, It is easy to show that the higher the moment, the more the amount of data required.
times that of mean, It is easy to show that the higher the moment, the more the amount of data required.
As noted earlier, turbulence problems are not usually Gaussian, and in fact values of the kurtosis substantionally greater than 3 are commonly encountered, especially for the moments of differentiated quantities. Clearly the non-Gaussian nature of random variables can affect the planning of experiments, since substantially greater amounts of data can be required to achieved the necessary statistical accuracy.
Credits
This text was based on "Lectures in Turbulence for the 21st Century" by Professor William K. George, Professor of Turbulence, Chalmers University of Technology, Gothenburg, Sweden.

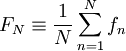
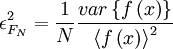
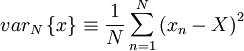
![\epsilon^{2}_{F_{N}}= \frac{1}{N} \frac{var \left\{ \left( x-X \right)^{2} - var \left[x \right] \right\} }{ \left( var \left\{ x \right\} \right)^{2} }](/W/images/math/1/7/1/1713ef52e0f0972c4e942738a206012b.png)
![var \left\{ \left( x- X \right)^{2} - var\left[x \right] \right\} = \left\langle \left( x- X \right)^{4} \right\rangle - \left[ var \left\{ x \right\} \right]^2](/W/images/math/f/d/a/fda59399bb14995d4520dc7b52f09efe.png)
![\epsilon^{2}_{var_{N}} = \frac{\left\langle \left( x- X \right)^4 \right\rangle}{\left[ var \left\{ x \right\} \right]^2 } - 1](/W/images/math/c/9/3/c93659bc771b229cc583b07ce8d97312.png)