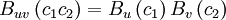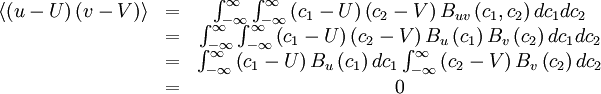Introduction to turbulence/Statistical analysis/Multivariate random variables
From CFD-Wiki
(→Statistical independence and lack of correlation) |
(→Statistical independence and lack of correlation) |
||
| Line 120: | Line 120: | ||
\left\langle \left(u-U \right) \left( v - V \right) \right\rangle & = & \int ^{\infty}_{-\infty} \int ^{\infty}_{-\infty} \left( c_{1} - U \right) \left( c_{2} - V \right) B_{uv} \left( c_{1} , c_{2} \right) dc_{1} dc_{2} \\ | \left\langle \left(u-U \right) \left( v - V \right) \right\rangle & = & \int ^{\infty}_{-\infty} \int ^{\infty}_{-\infty} \left( c_{1} - U \right) \left( c_{2} - V \right) B_{uv} \left( c_{1} , c_{2} \right) dc_{1} dc_{2} \\ | ||
& = & \int ^{\infty}_{-\infty} \int ^{\infty}_{-\infty} \left( c_{1} - U \right) \left( c_{2} - V \right) B_{u}\left(c_{1} \right) B_{v} \left( c_{2} \right) dc_{1} dc_{2} \\ | & = & \int ^{\infty}_{-\infty} \int ^{\infty}_{-\infty} \left( c_{1} - U \right) \left( c_{2} - V \right) B_{u}\left(c_{1} \right) B_{v} \left( c_{2} \right) dc_{1} dc_{2} \\ | ||
| - | & = & \int ^{\infty}_{-\infty} \int ^{\infty}_{-\infty} \\ | + | & = & \int ^{\infty}_{-\infty} \left(c_{1} - U \right) B_{u}\left(c_{1} \right) dc_{1} \int ^{\infty}_{-\infty} \left( c_{2} - V \right) B_{v} \left( c_{2} \right) dc_{2} \\ |
| + | & = & 0 | ||
\end{matrix} | \end{matrix} | ||
</math> | </math> | ||
</td><td width="5%">(2)</td></tr></table> | </td><td width="5%">(2)</td></tr></table> | ||
Revision as of 08:49, 5 June 2006
Joint pdfs and joint moments
Often it is importamt to consider more than one random variable at a time. For example, in turbulence the three components of the velocity vector are interralated and must be considered together. In addition to the marginal (or single variable) statistical moments already considered, it is necessary to consider the joint statistical moments.
For example if  and
and  are two random variables, there are three second-order moments which can be defined
are two random variables, there are three second-order moments which can be defined 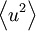 ,
, 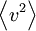 , and
, and 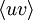 . The product moment
. The product moment 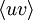 is called the cross-correlation or cross-covariance. The moments
is called the cross-correlation or cross-covariance. The moments 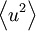 and
and 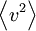 are referred to as the covariances, or just simply the variances. Sometimes
are referred to as the covariances, or just simply the variances. Sometimes 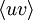 is also referred to as the correlation.
is also referred to as the correlation.
In a manner similar to that used to build-up the probabilility density function from its measurable counterpart, the histogram, a joint probability density function (or jpdf),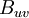 , can be built-up from the joint histogram. Figure 2.5 illustrates several examples of jpdf's which have different cross correlations. For convenience the fluctuating variables
, can be built-up from the joint histogram. Figure 2.5 illustrates several examples of jpdf's which have different cross correlations. For convenience the fluctuating variables 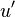 and
and 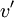 can be defined as
can be defined as
|
| (2) |
|
| (2) |
where as before capital letters are usd to represent the mean values. Clearly the fluctuating quantities 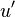 and
and 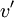 are random variables with zero mean.
are random variables with zero mean.
A positive value of 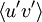 indicates that
indicates that 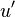 and
and 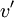 tend to vary together. A negative value indicates value indicates that when one variable is increasing the other tends to be decreasing. A zero value of
tend to vary together. A negative value indicates value indicates that when one variable is increasing the other tends to be decreasing. A zero value of 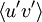 indicates that there is no correlation between
indicates that there is no correlation between 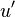 and
and 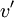 . As will be seen below, it does not mean that they are statistically independent.
. As will be seen below, it does not mean that they are statistically independent.
It is sometimes more convinient to deal with values of the cross-variances which have ben normalized by the appropriate variances. Thus the correlation coefficient is defined as:
|
| (2) |
The correlation coefficient is bounded by plus or minus one, the former representing perfect correlation and the latter perfect anti-correlation.
As with the single-variable pdf, there are certain conditions the joint probability density function must satisfy. If 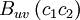 indicates the jpdf of the random variables
indicates the jpdf of the random variables 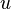 and
and 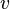 , then:
, then:
- Property 1
|
| (2) |
always
- Property 2
|
| (2) |
- Property 3
|
| (2) |
- Property 4
|
| (2) |
where 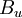 is a function of
is a function of 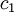 only
only
- Property 5
|
| (2) |
where 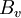 is a function of
is a function of 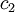 only
only
The functions 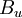 and
and 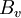 are called the marginal probability density functions and they are simply the single variable pdf's defined earlier. The subscript is used to indicate which variable is left after the others are integrated out. Note that
are called the marginal probability density functions and they are simply the single variable pdf's defined earlier. The subscript is used to indicate which variable is left after the others are integrated out. Note that 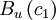 is not the same as
is not the same as 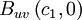 . The latter is only a slice through the
. The latter is only a slice through the 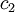 - axis, whale the marginal distribution is weighted by the integral of the distribution of the other variable. Figure 2.6. illustrates these differences.
- axis, whale the marginal distribution is weighted by the integral of the distribution of the other variable. Figure 2.6. illustrates these differences.
If the joint probability density function is known, the joint moments of all orders can be determined. Thus the 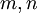 -th joint moment is
-th joint moment is
|
| (2) |
In the preceding discussions, only two random variables have been considered. The definitions, however, can easily be geberalized to accomodate any number of random variables. In addition, the joint statistics of a single random at different times or at different points in space could be considered. This will be done later when stationary and homogeneous random processes are considered.
The bi-variate normal (or Gaussian) distribution
If 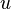 and
and 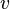 are normally distributed random variables with standard deviations given by
are normally distributed random variables with standard deviations given by 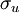 and
and 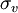 respectively , with correlation coefficient
respectively , with correlation coefficient 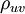 , then their joint probability density function is given by
, then their joint probability density function is given by
|
| (2) |
This distribution is plotted in Figure 2.7. for several values of 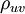 where
where 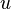 and
and 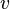 are assumed to be identically distributed (i.e.,
are assumed to be identically distributed (i.e., 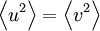 ).
).
It is straightforward to show (by completing the square and integrating) that this yields the single variable Gaussian distribution for the marginal distributions. It is also possible to write a multivariate Gaussian probability density function for any number of random variables.
Statistical independence and lack of correlation
Definition: Statistical Independence Two random variables are said to be statistically independent if their joint probability density is equal to the product of their marginal probability density functions. That is,
|
| (2) |
It is easy to see that statistical independence implies a complete lack of correlation; i.e., :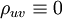 . From the definition of the cross-correlation
. From the definition of the cross-correlation
|
| (2) |

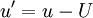
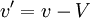
![\rho_{uv}\equiv \frac{ \left\langle u'v' \right\rangle}{ \left[ \left\langle u'^{2} \right\rangle \left\langle v'^{2} \right\rangle \right]^{1/2}}](/W/images/math/1/f/3/1f3881d311c8be1abd19cb613fa97e71.png)
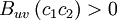
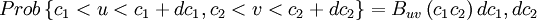
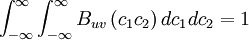
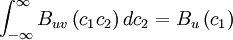
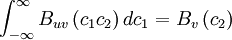
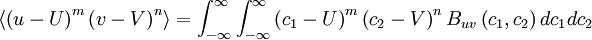
![B_{uvG} \left(c_{1},c_{2} \right) = \frac{1}{2 \pi \sigma_{u} \sigma_{v} }exp \left[ \frac{ \left( c_{1} - U \right)^{2} }{ 2\sigma^{2}_{u} } + \frac{ \left( c_{2}-V \right)^{2}}{2\sigma^{2}_{v} } - \rho_{uv}\frac{c_{1}c_{2}}{\sigma_{u} \sigma_{v}} \right]](/W/images/math/2/2/a/22a209918c145cefbbccc65ac82ca1c0.png)