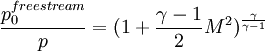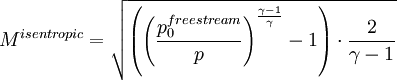Isentropic Mach number
From CFD-Wiki
(Difference between revisions)
m |
m |
||
| (One intermediate revision not shown) | |||
| Line 5: | Line 5: | ||
This gives the following formula for the isentropic Mach number: | This gives the following formula for the isentropic Mach number: | ||
| - | :<math>M^{isentropic} = \sqrt{ \left( ( \frac{p_0^{freestream}}{p} ) ^{\frac{\gamma - 1}{\gamma}} - 1 \right) \frac{2}{\gamma - 1}}</math> | + | :<math>M^{isentropic} = \sqrt{ \left( \left( \frac{p_0^{freestream}}{p} \right) ^{\frac{\gamma - 1}{\gamma}} - 1 \right) \cdot \frac{2}{\gamma - 1}}</math> |
Where: | Where: | ||
| Line 13: | Line 13: | ||
:<math>p</math> is the local [[Static pressure]]. | :<math>p</math> is the local [[Static pressure]]. | ||
| - | :<math>\gamma</math> is the [[ | + | :<math>\gamma</math> is the [[ratio of specific heats]], for air <math>\gamma = 1.4</math>. |
Latest revision as of 09:06, 16 August 2007
The isentropic Mach number is the Mach number you would have without any losses in the flow. This property is often used to investigate the ideal surface Mach number you would have without losses and walls without any friction (slip conditions). The isentropic Mach number is for example often plotted on turbomachinery blades. The isentropic Mach number can be computed from the isentropic flow relations using the following formula:
This gives the following formula for the isentropic Mach number:
Where:
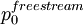 is the Total pressure in the freestream outside of the boundary layers. Usually the inlet total pressure is used.
is the Total pressure in the freestream outside of the boundary layers. Usually the inlet total pressure is used.
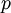 is the local Static pressure.
is the local Static pressure.
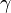 is the ratio of specific heats, for air
is the ratio of specific heats, for air 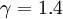 .
.