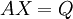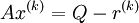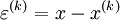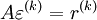Iterative methods
From CFD-Wiki
For solving a set of linear equations, we seek the solution to the problem:
After k iterations we obtain an approaximation to the solution as:
where 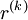 is the residual after k iterations.
is the residual after k iterations.
Defining:
as the difference between the exact and approaximate solution.
we obtain :
the purpose of iterations is to drive this residual to zero.