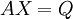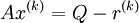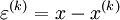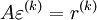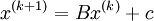Iterative methods
From CFD-Wiki
For solving a set of linear equations, we seek the solution to the problem:
After k iterations we obtain an approaximation to the solution as:
where 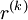 is the residual after k iterations.
is the residual after k iterations.
Defining:
as the difference between the exact and approaximate solution.
we obtain :
the purpose of iterations is to drive this residual to zero.
Stationary Iterative Methods
Iterative methods that can be expressed in the simple form:
When neither B nor c depend upon the iteration count (k), the iterative method is called stationary iterative method. Some of the stationary iterative methods are:
- Jacobi method
- Gauss-Seidel method
- Successive Overrelaxation (SOR) method and
- Symmetric Successive Overrelaxation (SSOR) method
Nonstationary Iterative Methods
When during the iterations B and c changes during the iterations, the method is called Nonstationary Iterative Method. Typically, constants B and c are computed by taking inner products of residuals or other vectors arising from the iterative method.
Some examples are:
- Conjugate Gradient Method (CG)
- MINRES and SYMMLQ
- Generalized Minimal Residual (GMRES)
- BiConjugate Gradient (BiCG)
- Quasi-Minimal Residual (QMR)
- Conjugate Gradient Squared Method (CGS)
- BiConjugate Gradient Stabilized (Bi-CGSTAB)
- Chebyshev Iteration