Kato-Launder modification
From CFD-Wiki
| Line 37: | Line 37: | ||
</math> | </math> | ||
| - | In incompressible flows, where <math>\frac{\partial u_i}{\partial x_i} = 0</math> the production term <math>P</math> can be rewritten as: | + | In incompressible flows, where <math>\frac{\partial u_i}{\partial x_i} = 0</math>, the production term <math>P</math> can be rewritten as: |
:<math> | :<math> | ||
\begin{matrix} | \begin{matrix} | ||
P & = & \tau_{ij}^{turb} \frac{\partial u_i}{\partial x_j} \\ | P & = & \tau_{ij}^{turb} \frac{\partial u_i}{\partial x_j} \\ | ||
| - | \ & = & \left[ 2 \mu_t S_{ij}^* - \frac{2}{3} \rho k \delta_{ij} | + | \ & = & \left[ 2 \mu_t S_{ij}^* - \frac{2}{3} \rho k \delta_{ij} \right] \frac{\partial u_i}{\partial x_j} \\ |
\ & = & \left[ 2 \mu_t \left( \frac{1}{2} \left(\frac{\partial u_i}{\partial x_j} + | \ & = & \left[ 2 \mu_t \left( \frac{1}{2} \left(\frac{\partial u_i}{\partial x_j} + | ||
| - | \frac{\partial u_j}{\partial x_i} \right) - \frac{1}{3} \frac{\partial u_k}{\partial x_k} \delta_{ij} \right) | + | \frac{\partial u_j}{\partial x_i} \right) - \frac{1}{3} \frac{\partial u_k}{\partial x_k} \delta_{ij} \right) |
| - | \right] \frac{\partial u_i}{\partial x_j} | + | - \frac{2}{3} \rho k \delta_{ij} |
| + | \right] \frac{\partial u_i}{\partial x_j} \\ | ||
| + | \ & \approx & \mbox{ (assuming incompressible flow)} \\ | ||
| + | \ & \approx & \mu_t \left(\frac{\partial u_i}{\partial x_j} + | ||
| + | \frac{\partial u_j}{\partial x_i} \right) \frac{\partial u_i}{\partial x_j} \\ | ||
| + | \ & = & | ||
\end{matrix} | \end{matrix} | ||
</math> | </math> | ||
Revision as of 15:21, 8 December 2005
The Kato-Launder modification is an ad-hoc modification of the turbulent production term in the k equation. The main purpose of the modification is to reduce the tendency that two-equation models have to over-predict the turbulent production in regions with large normal strain, i.e. regions with strong acceleration or decelleration.
The transport equation for the turbulent energy, 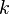 , used in most two-equation models can be written as:
, used in most two-equation models can be written as:
Where 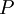 is the turbulent production normally given by:
is the turbulent production normally given by:
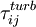 is the turbulent shear stress tensor given by the Boussinesq assumption:
is the turbulent shear stress tensor given by the Boussinesq assumption:
Where 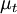 is the eddy-viscosity given by the turbluence model and
is the eddy-viscosity given by the turbluence model and 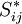 is the trace-less viscous strain-rate defined by:
is the trace-less viscous strain-rate defined by:
In incompressible flows, where 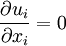 , the production term
, the production term 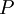 can be rewritten as:
can be rewritten as:
References
Kato, M. and Launder, B. E. (1993), "The Modeling of Turbulent Flow Around Stationary and Vibrating Square Cylinders", Proc. 9th Symposium on Turbulent Shear Flows, Kyoto, August 1993, pp. 10.4.1-10.4.6.

![\frac{\partial}{\partial t} \left( \rho k \right) +
\frac{\partial}{\partial x_j}
\left[
\rho k u_j - \left( \mu + \frac{\mu_t}{\sigma_k} \right)
\frac{\partial k}{\partial x_j}
\right]
=
P - \rho \epsilon - \rho D](/W/images/math/8/d/7/8d787db6600e44ff6855992620431595.png)
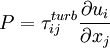
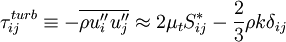
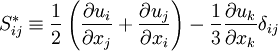
![\begin{matrix}
P & = & \tau_{ij}^{turb} \frac{\partial u_i}{\partial x_j} \\
\ & = & \left[ 2 \mu_t S_{ij}^* - \frac{2}{3} \rho k \delta_{ij} \right] \frac{\partial u_i}{\partial x_j} \\
\ & = & \left[ 2 \mu_t \left( \frac{1}{2} \left(\frac{\partial u_i}{\partial x_j} +
\frac{\partial u_j}{\partial x_i} \right) - \frac{1}{3} \frac{\partial u_k}{\partial x_k} \delta_{ij} \right)
- \frac{2}{3} \rho k \delta_{ij}
\right] \frac{\partial u_i}{\partial x_j} \\
\ & \approx & \mbox{ (assuming incompressible flow)} \\
\ & \approx & \mu_t \left(\frac{\partial u_i}{\partial x_j} +
\frac{\partial u_j}{\partial x_i} \right) \frac{\partial u_i}{\partial x_j} \\
\ & = &
\end{matrix}](/W/images/math/6/c/8/6c8d66bc1f8c4e47861759254947d92a.png)