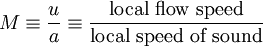Mach number
From CFD-Wiki
(Difference between revisions)
m |
|||
| (5 intermediate revisions not shown) | |||
| Line 4: | Line 4: | ||
:<math>M \equiv \frac{u}{a} \equiv \frac{\mbox{local flow speed}}{\mbox{local speed of sound}}</math> | :<math>M \equiv \frac{u}{a} \equiv \frac{\mbox{local flow speed}}{\mbox{local speed of sound}}</math> | ||
| - | The Mach number can be used to categorise | + | The Mach number can be used to categorise compressible flows into different [[Mach number regimes]]. To get a more physical insight into Mach number, it is useful if it is viewed as being proportional to the ratio of Kinetic energy to the internal energy of the molecules. |
| - | The name "Mach number" originates from the famous pioneer in compressible fluid dynamics [[Ernst Mach]] | + | On surfaces, like for example on turbomachinery blades, the [[isentropic Mach number]] is often of interest. |
| + | |||
| + | The name "Mach number" originates from the famous pioneer in compressible fluid dynamics [[Ernst Mach]]. | ||
[[Category: Dimensionless parameters]] | [[Category: Dimensionless parameters]] | ||
Latest revision as of 09:04, 16 August 2007
The Mach number, 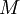 , is the local flow-speed,
, is the local flow-speed, 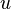 , divided by the local
speed of sound,
, divided by the local
speed of sound, 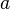 :
:
The Mach number can be used to categorise compressible flows into different Mach number regimes. To get a more physical insight into Mach number, it is useful if it is viewed as being proportional to the ratio of Kinetic energy to the internal energy of the molecules.
On surfaces, like for example on turbomachinery blades, the isentropic Mach number is often of interest.
The name "Mach number" originates from the famous pioneer in compressible fluid dynamics Ernst Mach.