Near-wall treatment for k-omega models
From CFD-Wiki
m |
m |
||
| Line 58: | Line 58: | ||
== References == | == References == | ||
| - | |||
* {{reference-paper|author=Menter, F., Esch, T.|year=2001|title=Elements of industrial heat transfer predictions|rest='COBEM 2001, 16th Brazilian Congress of Mechanical Engineering.'}} | * {{reference-paper|author=Menter, F., Esch, T.|year=2001|title=Elements of industrial heat transfer predictions|rest='COBEM 2001, 16th Brazilian Congress of Mechanical Engineering.'}} | ||
* {{reference-paper|author=ANSYS|year=2006|title=FLUENT Documentation|rest=''}} | * {{reference-paper|author=ANSYS|year=2006|title=FLUENT Documentation|rest=''}} | ||
Revision as of 22:26, 1 November 2011
As described in Two equation turbulence models low and high reynolds number treatments are possible.
Contents |
Standard wall functions
Main page: Two equation near-wall treatments
For  the boundary conditions imposed are
the boundary conditions imposed are
Moreover the centroid values in cells adjacent to solid wall are specified as
In the alternative approach  production terms is modified.
production terms is modified.
Automatic wall treatments
Menter suggested a mechanism that switches automatically between HRN and LRN treatments.
The full description to appear soon. The idea is based on blending:
FLUENT
Both k- omega models (std and sst) are available as low-Reynolds-number models as well as high-Reynolds-number models.
The wall boundary conditions for the k equation in the k- omega models are treated in the same way as the k equation is treated when enhanced wall treatments are used with the k- epsilon models.
This means that all boundary conditions for
- wall-function meshes will correspond to the wall function approach, while for the
- fine meshes, the appropriate low-Reynolds-number boundary conditions will be applied.
In Fluent, that means:
If the Transitional Flows option is enabled in the Viscous Model panel, low-Reynolds-number variants will be used, and, in that case, mesh guidelines should be the same as for the enhanced wall treatment
(y+ at the wall-adjacent cell should be on the order of y+ = 1. However, a higher y+ is acceptable as long as it is well inside the viscous sublayer (y+ < 4 to 5).)
If Transitional Flows option is not active, then the mesh guidelines should be the same as for the wall functions.
(For [...] wall functions, each wall-adjacent cell's centroid should be located within the log-law layer, 30 < y+ < 300. A y+ value close to the lower bound y+ = 30 is most desirable.)
References
- Menter, F., Esch, T. (2001), "Elements of industrial heat transfer predictions", 'COBEM 2001, 16th Brazilian Congress of Mechanical Engineering.'.
- ANSYS (2006), "FLUENT Documentation", .

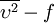 model
model
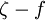 model
model
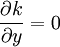
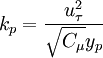
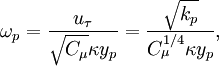
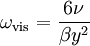
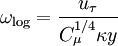
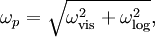
![u_\tau = \sqrt[4]{(u_\tau^{\text{vis}})^4 + (u_\tau^{\text{log}})^4},](/W/images/math/8/6/d/86dc5093c131963cbd5a3a4e0e74dfd1.png)