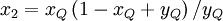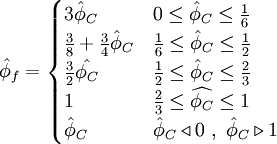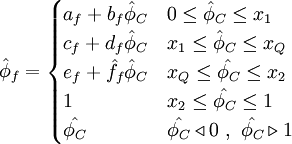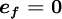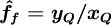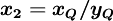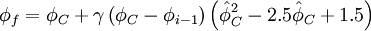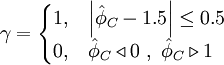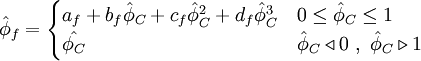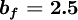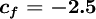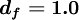From CFD-Wiki
QUICKER - Quadratic Upwind Interpolation Extended and Revised
SMART - Sharp and Monotonic Algorithm for Realistic Transport (Also CCCT - Curvature-Compensated Convective Transport )
P.H.Gaskell and A.C.K. Lau, Curvature-compensated convective transport: SMART, a new boundedness preserving transport algorithm, International J. Numer. Methods Fluids 8 (1988) 617-641
Normalized variables - uniform grids (NVD)
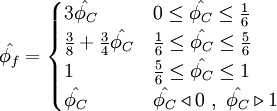
| (2) |
Normalized variables - non-uniform grids (NVSF)
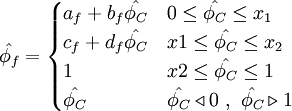
| (2) |
where
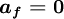
| (2) |
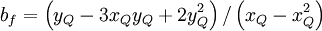
| (2) |
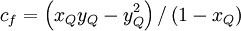
| (2) |
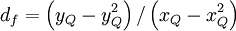
| (2) |
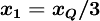
| (2) |
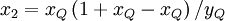
| (2) |
SMARTER - SMART Efficiently Revised
J.K. Shin and Y.D. Choi
Study on the improvement of the convective differencing scheme for the high-accuracy and stable resolution of the numerical solution
Trans. KSME 16(6) (1992) 1179-1194 (in Korean)
Normalized variables - uniform grids
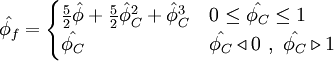
| (2) |
Normalized variables - non-uniform grids
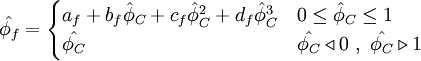
| (2) |
where
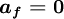
| (2) |
![b_{f}= \left[ x^{4}_{Q} + s_{Q} \left( x^{3}_{Q} - x^{2}_{Q} \right) + y_{Q} \left( 2 x_{Q} -3 x^{2}_{Q} \right) \right] / \left( x_{Q} - x^{2}_{Q} \right)^2](/W/images/math/5/d/e/5de8626e1740c88ec4fa2556b9914406.png)
| (2) |
![c_{f}= \left[ - 2 x^{3}_{Q} + s_{Q} \left( x_{Q} - x^{3}_{Q} \right) + y_{Q} \left( 3 x^{2}_{Q} - 1 \right) \right] / \left( x_{Q} - x^{2}_{Q} \right)^2](/W/images/math/8/b/9/8b9edc6af8724dc91298025c5aac15d6.png)
| (2) |
![d_{f} = \left[ x^{2}_{Q} + s_{Q} \left( x^{2}_{Q} - x_{Q} \right) + y_{Q} \left( 1 - 2 x_{Q} \right) \right] / \left( x_{Q} - x^{2}_{Q} \right)^2](/W/images/math/c/5/c/c5c068cf51f211e64967d31daa6a6aa5.png)
| (2) |
WACEB
Song B., Liu G.B., Kam K.Y., Amano R.S.
On a higher-order bounded discretization schemes
International Journal for Numerical Methods in Fluids, 2000, 32, 881-897
Normalized variables - uniform grids
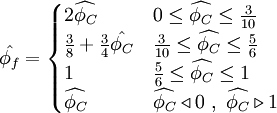
| (2) |
Normalized variables - non-uniform grids
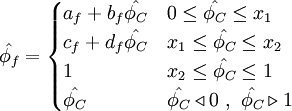
| (2) |
where
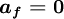
| (2) |
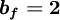
| (2) |
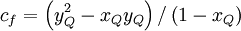
| (2) |
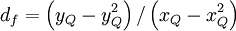
| (2) |
![x_{1}=x_{Q}y_{Q} \left( y_{Q} - x_{Q} \right)/ \left[ 2 x_{Q} \left( 1 - x_{Q} \right) - y_{Q} \left( 1 - y_{Q} \right) \right]](/W/images/math/1/e/7/1e761d03588aa4df8375b382e9450a3c.png)
| (2) |
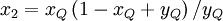
| (2) |
VONOS - Variable-Order Non-Oscillatory Scheme
Varonos A., Bergeles G., Development and assessment of a Variable-Order Non-oscillatory Scheme for convection term discretization // International Journal for Numerical Methods in Fluids. 1998. 26, N 1. 1-16
Normalized variables - uniform grids
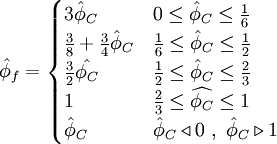
| (2) |
Normalized variables - non-uniform grids
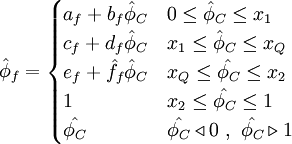
| (2) |
where
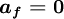
| (2) |
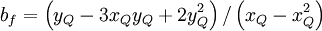
| (2) |
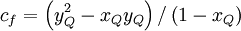
| (2) |
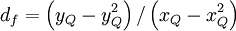
| (2) |
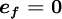
| (2) |
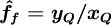
| (2) |
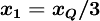
| (2) |
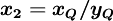
| (2) |
CHARM - Cubic / Parabolic High-Accuracy Resolution Method
G.Zhou , Numerical simulations of physical discontinuities in single and multi-fluid flows for arbitrary Mach numbers, PhD Thesis, Chalmers University of Technology, Sweden (1995)
Gang Zhou, Lars Davidson and Erik Olsson
Transonic Inviscid / Turbulent Airfoil Flow Simulations Using a Pressure Based Method with High Order Schemes
Lecture notes in Physics, No. 453, pp. 372-377, Springler-Verlag, Berlin, (1995)
usual variables
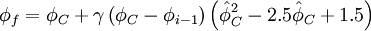
| (2) |
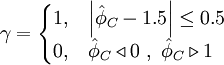
| (2) |
normalised variables (uniform grids)
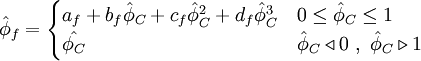
| (2) |
where
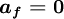
| (2) |
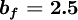
| (2) |
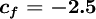
| (2) |
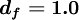
| (2) |
Normalized variables - non-uniform grids
unfortunately we cen't present expression on non-uniform grids because of complexity
UMIST - Upstream Monotonic Interpolation for Scalar Transport
F.S.Lien and M.A.Leschziner , Upstream Monotonic Interpolation for Scalar Transport with application to complex turbulent flows, International Journal for Numerical Methods in Fluids, Vol. 19, p.257, (1994)
Return to Numerical Methods
Return to Approximation Schemes for convective term - structured grids

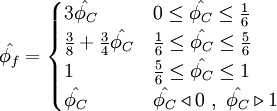
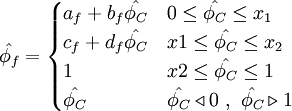
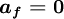
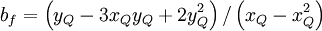
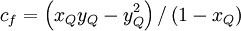
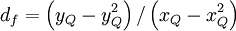
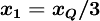
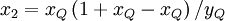
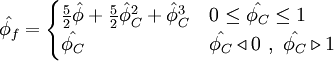
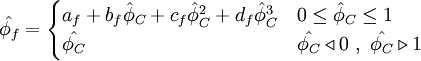
![b_{f}= \left[ x^{4}_{Q} + s_{Q} \left( x^{3}_{Q} - x^{2}_{Q} \right) + y_{Q} \left( 2 x_{Q} -3 x^{2}_{Q} \right) \right] / \left( x_{Q} - x^{2}_{Q} \right)^2](/W/images/math/5/d/e/5de8626e1740c88ec4fa2556b9914406.png)
![c_{f}= \left[ - 2 x^{3}_{Q} + s_{Q} \left( x_{Q} - x^{3}_{Q} \right) + y_{Q} \left( 3 x^{2}_{Q} - 1 \right) \right] / \left( x_{Q} - x^{2}_{Q} \right)^2](/W/images/math/8/b/9/8b9edc6af8724dc91298025c5aac15d6.png)
![d_{f} = \left[ x^{2}_{Q} + s_{Q} \left( x^{2}_{Q} - x_{Q} \right) + y_{Q} \left( 1 - 2 x_{Q} \right) \right] / \left( x_{Q} - x^{2}_{Q} \right)^2](/W/images/math/c/5/c/c5c068cf51f211e64967d31daa6a6aa5.png)
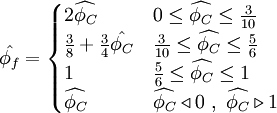
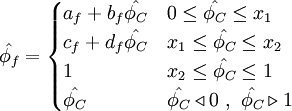
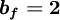
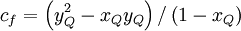
![x_{1}=x_{Q}y_{Q} \left( y_{Q} - x_{Q} \right)/ \left[ 2 x_{Q} \left( 1 - x_{Q} \right) - y_{Q} \left( 1 - y_{Q} \right) \right]](/W/images/math/1/e/7/1e761d03588aa4df8375b382e9450a3c.png)