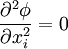Potential flow
From CFD-Wiki
(Difference between revisions)
(Really dead link, which is pointing to a not so honest website...) |
|||
| (2 intermediate revisions not shown) | |||
| Line 15: | Line 15: | ||
== Governing equations == | == Governing equations == | ||
| + | In the case of an incompressible flow, <math>\phi</math> satisfies the Laplace equation. | ||
| - | + | From the continuity equation, we get: | |
| - | = | + | :<math> |
| - | + | \frac{\partial^2 \phi}{\partial x_i^2}=0 | |
| + | </math> | ||
Latest revision as of 13:06, 16 March 2016
A flow in which vorticity is zero is called potential flow, or irrotational flow. Since the vorticity is zero
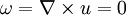
it implies that the velocity is the gradient of a scalar field called the velocity potential, and usually denoted as 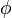
At high Reynolds numbers, flow past slender bodies is attached (no boundary layer separation) and the boundary layers are thin. In such situations vorticity is confined to the thin boundary layers and the rest of the flow is irrotational.
Governing equations
In the case of an incompressible flow, 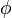 satisfies the Laplace equation.
satisfies the Laplace equation.
From the continuity equation, we get: