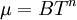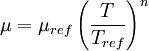Power-law viscosity law
From CFD-Wiki
A power-law can be used as an approximation of the viscosity of dilute gases. For dilute gases at moderate temperatures this formula is slightly less accurate than Sutherland's law. The power-law viscosity law can be written as:
Where 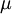 is the viscosity in kg/m-s,
is the viscosity in kg/m-s, 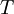 is the static temperature in K, and
is the static temperature in K, and 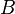 is a dimensional coefficient. For air at moderate temperatures and pressures
is a dimensional coefficient. For air at moderate temperatures and pressures 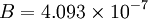 , and
, and 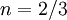 .
.
The power-law viscosity law can also be written as:
Where 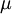 is the viscosity in kg/m-s,
is the viscosity in kg/m-s, 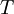 is the static temperature in K,
is the static temperature in K, 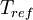 is a reference value in K,
is a reference value in K, 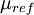 is a reference value in kg/m-s. For air at moderate temperatures and pressures,
is a reference value in kg/m-s. For air at moderate temperatures and pressures, 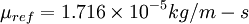 ,
, 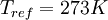 , and
, and 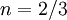 .
.
Note that there exists a different power-law for non-Newtonian fluids!