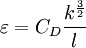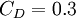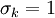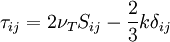Prandtl's one-equation model
From CFD-Wiki
(Difference between revisions)
| Line 22: | Line 22: | ||
\sigma _k = 1 | \sigma _k = 1 | ||
</math> <br> | </math> <br> | ||
| + | |||
| + | |||
| + | where <br> | ||
| + | :<math> | ||
| + | \tau _{ij} = 2\nu _T S_{ij} - {2 \over 3}k\delta _{ij} | ||
| + | </math> | ||
== References == | == References == | ||
#{{reference-book|author=Wilcox, D.C. |year=2004|title=Turbulence Modeling for CFD|rest=ISBN 1-928729-10-X, 2nd Ed., DCW Industries, Inc.}} | #{{reference-book|author=Wilcox, D.C. |year=2004|title=Turbulence Modeling for CFD|rest=ISBN 1-928729-10-X, 2nd Ed., DCW Industries, Inc.}} | ||
Revision as of 09:34, 26 September 2005
Contents |
Kinematic Eddy Viscosity
Model
Closure Coefficients and Auxilary Relations
where
References
- Wilcox, D.C. (2004), Turbulence Modeling for CFD, ISBN 1-928729-10-X, 2nd Ed., DCW Industries, Inc..

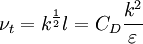
![{{\partial k} \over {\partial t}} = U_j {{\partial k} \over {\partial x_j }} = \tau _{ij} {{\partial U_i } \over {\partial x_j }} - C_D {{k^{{3 \over 2}} } \over l} + {\partial \over {\partial x_j }}\left[ {\left( {\nu + {{\nu _T } \over {\sigma _k }}} \right){{\partial k} \over {\partial x_j }}} \right]](/W/images/math/e/2/f/e2f56eb7e46e14a52bf870d57b0c22fe.png)