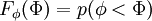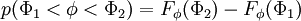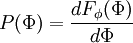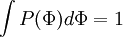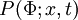Probability density function
From CFD-Wiki
Stochastic methods use distribution functions to decribe the fluctuacting scalars in a turbulent field.
The distribution function 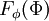 of a scalar
of a scalar 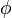 is the probability
is the probability
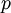 of finding a value of
of finding a value of 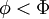
The probability of finding 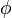 in a range
in a range 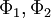 is
is
The probability density function (PDF) is
where 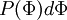 is the probability of
is the probability of 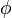 being in the range
being in the range 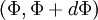 . It follows that
. It follows that
Integrating over all the possible values of 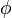 .
The PDF of any stochastic variable depends "a-priori" on space and time.
.
The PDF of any stochastic variable depends "a-priori" on space and time.