Rhie-Chow interpolation
From CFD-Wiki
we have at each cell descretised equation in this form,
 ;
;
we have
For continuity :
so we get:
this gives us:
defining 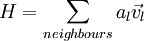
from this a pressure correction equation could be formed as:
This is a poisson equation.
Here the gradients could be used from previous iteration.


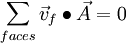
![\left[ {\frac{{\sum\limits_{neighbours} {a_l } \vec v_l }}{{a_p }}} \right]_{face} - \left[ {\frac{{\nabla p}}{{a_p V}}} \right]_{face} = 0](/W/images/math/f/7/e/f7e0da565cdb617ce4f3124203e503c1.png)
![\left[ {\frac{{\sum\limits_{neighbours} {a_l } \vec v_l }}{{a_p }}} \right]_{face} = \left[ {\frac{{\nabla p}}{{a_p V}}} \right]_{face}](/W/images/math/d/9/a/d9a701a1aaad2b208b62474614781147.png)
![\left[ {\frac{1}{{a_p }}H} \right]_{face} = \left[ {\frac{1}{{a_p }}\frac{{\nabla p}}{V}} \right]_{face}](/W/images/math/b/e/1/be109456135e08608800a492d37b823a.png)
![\left[ {\frac{1}{{a_p }}H} \right]_{face} - \left[ {\frac{1}{{a_p }}\frac{{\nabla p^* }}{V}} \right]_{face} = \left[ {\frac{1}{{a_p }}\frac{{\nabla p^' }}{V}} \right]_{face}](/W/images/math/0/4/3/043590859f53e135dd2724fe98e03b71.png)