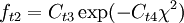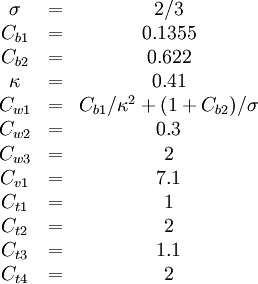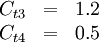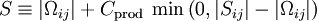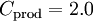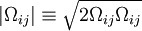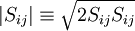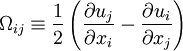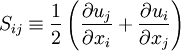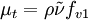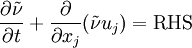Spalart-Allmaras model
From CFD-Wiki
(split a long equation into two lines) |
Tohoughton (Talk | contribs) (→Boundary conditions) |
||
| Line 106: | Line 106: | ||
== Boundary conditions == | == Boundary conditions == | ||
| + | Boundary conditions are set by defining values of <math>\tilde{\nu}</math>. This may be refered to as the Spalart-Allmaras variable. | ||
| + | |||
Walls: <math>\tilde{\nu}=0</math> | Walls: <math>\tilde{\nu}=0</math> | ||
| Line 111: | Line 113: | ||
Outlet: convective outlet. | Outlet: convective outlet. | ||
| + | |||
| + | To calculate boundary conditions for this model based on experimental measurements see [[Turbulence free-stream boundary conditions|turbulence free-stream boundary conditions]]. | ||
== References == | == References == | ||
Revision as of 09:54, 15 May 2008
Spalart-Allmaras model is a one equation model for the turbulent viscosity.
Contents |
Original model
The turbulent eddy viscosity is given by
where
- d is the distance to the closest surface
The constants are
Modifications to original model
According to Spalart it is safer to use the following values for the last two constants:
[Dacles-Mariani et. al. 1995] proposed a modification of the model which also accounts for the effect of mean strain rate on turbulence production. This modification instead prescribes:
where
Other models related to the S-A model:
DES (1999) [1]
DDES (2006)
Model for compressible flows
There are two approaches to adapting the model for compressible flows. In the first approach the turbulent dynamic viscosity is computed from
where 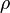 is the local density. The convective terms in the equation for
is the local density. The convective terms in the equation for 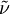 are modified to
are modified to
where the right hand side (RHS) is the same as in the original model.
Boundary conditions
Boundary conditions are set by defining values of 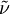 . This may be refered to as the Spalart-Allmaras variable.
. This may be refered to as the Spalart-Allmaras variable.
Walls: 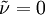
Freestream: Ideally 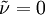 , but some solvers can have problem with that so
, but some solvers can have problem with that so 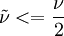 can be used. This is if the trip term is used to "start up" the model. A convenient option is to set
can be used. This is if the trip term is used to "start up" the model. A convenient option is to set 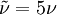 in the freestream. The model then provides fully turbulent results and any regions like boundary layers that contain shear become fully turbulent.
in the freestream. The model then provides fully turbulent results and any regions like boundary layers that contain shear become fully turbulent.
Outlet: convective outlet.
To calculate boundary conditions for this model based on experimental measurements see turbulence free-stream boundary conditions.
References
- Dacles-Mariani, J., Zilliac, G. G., Chow, J. S. and Bradshaw, P. (1995), "Numerical/Experimental Study of a Wingtip Vortex in the Near Field", AIAA Journal, 33(9), pp. 1561-1568, 1995.
- Spalart, P. R. and Allmaras, S. R. (1992), "A One-Equation Turbulence Model for Aerodynamic Flows", AIAA Paper 92-0439.
- Spalart, P. R. and Allmaras, S. R. (1994), "A One-Equation Turbulence Model for Aerodynamic Flows", La Recherche Aerospatiale n 1, 5-21.

 model
model
 model
model
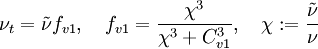
![\begin{matrix}
\frac{\partial \tilde{\nu}}{\partial t} + u_j \frac{\partial \tilde{\nu}}{\partial x_j} & = & C_{b1} [1 - f_{t2}] \tilde{S} \tilde{\nu} + \frac{1}{\sigma} \{ \nabla \cdot [(\nu + \tilde{\nu}) \nabla \tilde{\nu}] + C_{b2} | \nabla \nu |^2 \} - \\
\ & \ & \left[C_{w1} f_w - \frac{C_{b1}}{\kappa^2} f_{t2}\right] \left( \frac{\tilde{\nu}}{d} \right)^2 + f_{t1} \Delta U^2 \\
\end{matrix}](/W/images/math/6/8/6/6862e971bbdc4ecba669c49b9d5fc2ee.png)
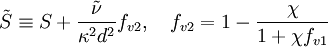
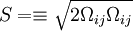
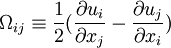
![f_w = g \left[ \frac{ 1 + C_{w3}^6 }{ g^6 + C_{w3}^6 } \right]^{1/6}, \quad g = r + C_{w2}(r^6 - r), \quad r \equiv \frac{\tilde{\nu} }{ \tilde{S} \kappa^2 d^2 }](/W/images/math/0/9/b/09b19885ed6dffe3dec850e2516f1696.png)
![f_{t1} = C_{t1} g_t \exp\left( -C_{t2} \frac{\omega_t^2}{\Delta U^2} [ d^2 + g^2_t d^2_t] \right)](/W/images/math/9/9/3/993b41d0ba795e0b3877d041c4cff1cb.png)