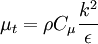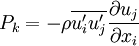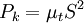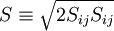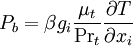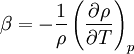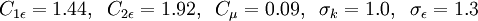Standard k-epsilon model
From CFD-Wiki
(Difference between revisions)
Littleandy (Talk | contribs) |
(→Transport equations for standard <math>k</math>-<math>\epsilon</math> model) |
||
| (3 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
| + | {{Turbulence modeling}} | ||
| + | |||
== Transport equations for standard k-epsilon model == | == Transport equations for standard k-epsilon model == | ||
| - | For k <br> | + | For turbulent kinetic energy <math> k </math> <br> |
:<math> \frac{\partial}{\partial t} (\rho k) + \frac{\partial}{\partial x_i} (\rho k u_i) = \frac{\partial}{\partial x_j} \left[ \left(\mu + \frac{\mu_t}{\sigma_k} \right) \frac{\partial k}{\partial x_j}\right] + P_k + P_b - \rho \epsilon - Y_M + S_k </math> | :<math> \frac{\partial}{\partial t} (\rho k) + \frac{\partial}{\partial x_i} (\rho k u_i) = \frac{\partial}{\partial x_j} \left[ \left(\mu + \frac{\mu_t}{\sigma_k} \right) \frac{\partial k}{\partial x_j}\right] + P_k + P_b - \rho \epsilon - Y_M + S_k </math> | ||
Revision as of 15:16, 21 June 2007
Contents |
Transport equations for standard k-epsilon model
For turbulent kinetic energy 
For dissipation 
Modeling turbulent viscosity
Turbulent viscosity is modelled as:
Production of k
Where 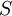 is the modulus of the mean rate-of-strain tensor, defined as :
is the modulus of the mean rate-of-strain tensor, defined as :
Effect of buoyancy
where Prt is the turbulent Prandtl number for energy and gi is the component of the gravitational vector in the ith direction. For the standard and realizable - models, the default value of Prt is 0.85.
The coefficient of thermal expansion,  , is defined as
, is defined as

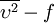 model
model
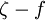 model
model
![\frac{\partial}{\partial t} (\rho k) + \frac{\partial}{\partial x_i} (\rho k u_i) = \frac{\partial}{\partial x_j} \left[ \left(\mu + \frac{\mu_t}{\sigma_k} \right) \frac{\partial k}{\partial x_j}\right] + P_k + P_b - \rho \epsilon - Y_M + S_k](/W/images/math/0/3/3/03313e8802538459d0a202c34efc1274.png)
![\frac{\partial}{\partial t} (\rho \epsilon) + \frac{\partial}{\partial x_i} (\rho \epsilon u_i) = \frac{\partial}{\partial x_j} \left[\left(\mu + \frac{\mu_t}{\sigma_{\epsilon}} \right) \frac{\partial \epsilon}{\partial x_j} \right] + C_{1 \epsilon}\frac{\epsilon}{k} \left( P_k + C_{3 \epsilon} P_b \right) - C_{2 \epsilon} \rho \frac{\epsilon^2}{k} + S_{\epsilon}](/W/images/math/0/6/c/06ca9efd2f29b3816707de0452572c77.png)