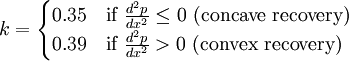Stratford's separation criterion
From CFD-Wiki
(Difference between revisions)
(not finished yet) |
(still not finished) |
||
| Line 1: | Line 1: | ||
| - | Stratford's separation criteria is an old classical analytical way to assess if a boundary layer is likely to separate or not. Stratford's criteria says that from the start of the pressure recovery | + | Stratford's separation criteria is an old classical analytical way to assess if a turbulent boundary layer is likely to separate or not. Stratford's criteria says that from the start of the pressure recovery where the max velocity and the minimum static pressure is obtained the boundary layer is on the verge of separation when: |
<math> | <math> | ||
| Line 5: | Line 5: | ||
</math> | </math> | ||
| - | + | This formula is only valid as long as <math>C'_p < \frac{4}{7}</math>. | |
| - | <math>C'_p</math> is the canonical pressure distribution defined by: | + | *<math>C'_p</math> is the canonical pressure distribution defined by: |
:<math>C'_p = 1 - \left( \frac{U}{U_{max}} \right) ^ 2</math> | :<math>C'_p = 1 - \left( \frac{U}{U_{max}} \right) ^ 2</math> | ||
:<math>U</math> is the local velocity and <math>U_{max}</math> is the maximum velocity at the start of the pressure recovery. | :<math>U</math> is the local velocity and <math>U_{max}</math> is the maximum velocity at the start of the pressure recovery. | ||
| - | <math>x'</math> is the effective length of the boundary layer. Note that computing <math>x'</math> can be a bit tricky. If the boundary layer is first accelerated up to the start of the recovery a turbulent boundary layer can be assumed to have the followig effective length: | + | *<math>k</math> is a constant which Stratford used the following values for: |
| + | :<math> | ||
| + | k = | ||
| + | \begin{cases} | ||
| + | 0.35 & \mbox{if } \frac{d^2p}{dx^2} \le 0 \mbox{ (concave recovery)} \\ | ||
| + | 0.39 & \mbox{if } \frac{d^2p}{dx^2} > 0 \mbox{ (convex recovery)} | ||
| + | \end{cases} | ||
| + | </math> | ||
| + | |||
| + | *<math>x'</math> is the effective length of the boundary layer. Note that computing <math>x'</math> can be a bit tricky. If the boundary layer is first accelerated up to the start of the recovery a turbulent boundary layer can be assumed to have the followig effective length: | ||
| + | |||
| + | Stratford's separation criteria is known to be conservative. It will most likely predict a bit too early separation. | ||
Revision as of 12:15, 13 February 2008
Stratford's separation criteria is an old classical analytical way to assess if a turbulent boundary layer is likely to separate or not. Stratford's criteria says that from the start of the pressure recovery where the max velocity and the minimum static pressure is obtained the boundary layer is on the verge of separation when:
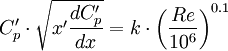
This formula is only valid as long as 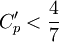 .
.
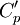 is the canonical pressure distribution defined by:
is the canonical pressure distribution defined by:
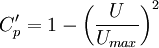
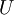 is the local velocity and
is the local velocity and 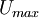 is the maximum velocity at the start of the pressure recovery.
is the maximum velocity at the start of the pressure recovery.
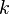 is a constant which Stratford used the following values for:
is a constant which Stratford used the following values for:
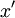 is the effective length of the boundary layer. Note that computing
is the effective length of the boundary layer. Note that computing 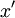 can be a bit tricky. If the boundary layer is first accelerated up to the start of the recovery a turbulent boundary layer can be assumed to have the followig effective length:
can be a bit tricky. If the boundary layer is first accelerated up to the start of the recovery a turbulent boundary layer can be assumed to have the followig effective length:
Stratford's separation criteria is known to be conservative. It will most likely predict a bit too early separation.