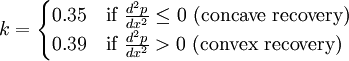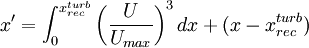Stratford's separation criterion
From CFD-Wiki
(Difference between revisions)
m (Stratford's separation criteria moved to Stratford's separation criterion: Incorrect title) |
(still more to add) |
||
| Line 21: | Line 21: | ||
</math> | </math> | ||
| - | *<math>x'</math> is the effective length of the boundary layer. Note that computing <math>x'</math> can be a bit tricky. If the boundary layer is first accelerated up to the start of the recovery a turbulent boundary layer can be assumed to have the followig effective length: | + | *<math>x'</math> is the effective length of the boundary layer. Note that computing <math>x'</math> can be a bit tricky. If the boundary layer is first accelerated up to the start of the recovery and is assumed to be turbulent all the time a turbulent boundary layer can be assumed to have the followig effective length: |
| + | :<math>x' = \int_0^{x^{turb}_{rec}} \left( \frac{U}{U_{max}} \right) ^ 3 dx + (x - x^{turb}_{rec})</math> | ||
| + | Note that this is only valid if the approaching boundary layer can be assumed to be fully turbulent. If the boundary layer is laminar, or undergoes transition, a different approximations needs to be done. | ||
Stratford's separation criteria is known to be conservative. It will most likely predict a bit too early separation. | Stratford's separation criteria is known to be conservative. It will most likely predict a bit too early separation. | ||
Revision as of 17:54, 14 February 2008
Stratford's separation criteria is an old classical analytical way to assess if a turbulent boundary layer is likely to separate or not. Stratford's criteria says that from the start of the pressure recovery where the max velocity and the minimum static pressure is obtained the boundary layer is on the verge of separation when:
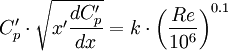
This formula is only valid as long as 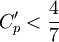 .
.
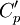 is the canonical pressure distribution defined by:
is the canonical pressure distribution defined by:
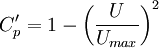
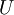 is the local velocity and
is the local velocity and 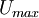 is the maximum velocity at the start of the pressure recovery.
is the maximum velocity at the start of the pressure recovery.
 is a constant which Stratford used the following values for:
is a constant which Stratford used the following values for:
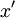 is the effective length of the boundary layer. Note that computing
is the effective length of the boundary layer. Note that computing 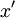 can be a bit tricky. If the boundary layer is first accelerated up to the start of the recovery and is assumed to be turbulent all the time a turbulent boundary layer can be assumed to have the followig effective length:
can be a bit tricky. If the boundary layer is first accelerated up to the start of the recovery and is assumed to be turbulent all the time a turbulent boundary layer can be assumed to have the followig effective length:
Note that this is only valid if the approaching boundary layer can be assumed to be fully turbulent. If the boundary layer is laminar, or undergoes transition, a different approximations needs to be done.
Stratford's separation criteria is known to be conservative. It will most likely predict a bit too early separation.