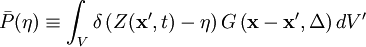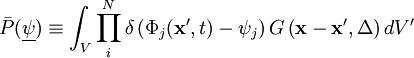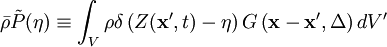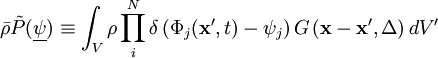Subgrid PDF
From CFD-Wiki
A subgrid probability density function 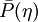 ,
also known as filtered density function (FDF),
is the distribution function of scalar
,
also known as filtered density function (FDF),
is the distribution function of scalar 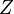 at subgrid scales.
at subgrid scales.
The probability of observing values between 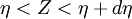 within the filter volume is
within the filter volume is 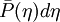
where 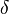 is the Dirac delta function,
is the Dirac delta function,
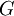 is a positive defined filter function
with filter width
is a positive defined filter function
with filter width 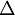 .
.
The joint subgrid PDF of 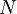 scalars is
scalars is
where 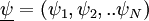 is the phase space for the scalar variables
is the phase space for the scalar variables
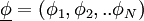 .
.
A density weighted FDF, 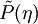 , can be obtained as
, can be obtained as
and in the same manner for the joint FDF