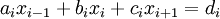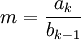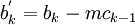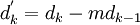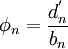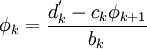Tridiagonal matrix algorithm - TDMA (Thomas algorithm)
From CFD-Wiki
(Difference between revisions)
(towards a uniform notation for linear systems : A*Phi = B) |
m (→Introduction) |
||
| Line 1: | Line 1: | ||
== Introduction == | == Introduction == | ||
| - | The Thomas Algorithm is a special form of | + | The Thomas Algorithm is a special form of Gaussian elimination that can be used to solve tridiagonal |
| - | systems of equations. When the matrix is tridiagonal, the solution can be obtained in O(n) operations, | + | systems of equations. When the matrix is tridiagonal, the solution can be obtained in <math>O(n)</math> operations, |
| - | instead of O( | + | instead of <math>O(n^3)</math>. Example of such matrices are matrices arising from discretization of 1D problems. |
We can write the tri-diagonal system in the form: <br> | We can write the tri-diagonal system in the form: <br> | ||
:<math> | :<math> | ||
| - | a_i | + | a_i x_{i - 1} + b_i x_i + c_i x_{i + 1} = d_i |
</math> <br> | </math> <br> | ||
Where <math> a_1 = 0 </math> and <math> c_n = 0 </math> <br> | Where <math> a_1 = 0 </math> and <math> c_n = 0 </math> <br> | ||
Revision as of 23:01, 18 December 2005
Introduction
The Thomas Algorithm is a special form of Gaussian elimination that can be used to solve tridiagonal
systems of equations. When the matrix is tridiagonal, the solution can be obtained in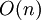 
operations,
instead of 
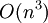. Example of such matrices are matrices arising from discretization of 1D problems.
We can write the tri-diagonal system in the form:
Where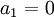 
and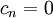 
Algorithm
- for k:= 2 step until n do
-
- end loop (k)
- then
-
- for k := n-1 stepdown until 1 do
-
- end loop (k)
References
- Conte, S.D., and deBoor, C. (1972), Elementary Numerical Analysis, McGraw-Hill, New York..
Return to Numerical Methods
