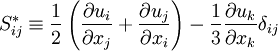Turbulence dissipation rate
From CFD-Wiki
(Difference between revisions)
m (moved Turbulence dissipation to Turbulence dissipation rate: more complete name) |
Pete Bachant (Talk | contribs) (Abbreviations for units no longer italicized.) |
||
| (One intermediate revision not shown) | |||
| Line 1: | Line 1: | ||
| - | Turbulence dissipation, <math>\epsilon</math> is the rate at which [[turbulence kinetic energy]] is converted into thermal internal energy. The SI unit of <math>\epsilon</math> is <math>J / kg s = m^2 / s^3</math>. | + | Turbulence dissipation, <math>\epsilon</math> is the rate at which [[turbulence kinetic energy]] is converted into thermal internal energy. The SI unit of <math>\epsilon</math> is <math>\mathrm{J} / (\mathrm{kg} \cdot \mathrm{s}) = \mathrm{m}^2 / \mathrm{s}^3</math>. |
<math>\epsilon \, \equiv \, \nu \overline{\frac{\partial u_i'}{\partial x_k}\frac{\partial u_i'}{\partial x_k}}</math> | <math>\epsilon \, \equiv \, \nu \overline{\frac{\partial u_i'}{\partial x_k}\frac{\partial u_i'}{\partial x_k}}</math> | ||
| + | |||
| + | |||
| + | For compressible flows the definition is most often slightly different: | ||
| + | |||
| + | <math>\epsilon \, \equiv \, \frac{1}{\overline{\rho}} \overline{\tau_{ij} \frac{\partial u_i''}{\partial x_j}}</math> | ||
| + | |||
| + | Where the viscous stress, <math>\tau_{ij}</math>, using Stokes law for mono-atomic gases, is given by: | ||
| + | |||
| + | <math>\tau_{ij} = 2 \mu S^*_{ij}</math> | ||
| + | |||
| + | where | ||
| + | |||
| + | <math>S^*_{ij} \equiv \frac{1}{2} \left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i} \right) - \frac{1}{3} \frac{\partial u_k}{\partial x_k} \delta_{ij}</math> | ||
Latest revision as of 01:00, 11 April 2015
Turbulence dissipation,  is the rate at which turbulence kinetic energy is converted into thermal internal energy. The SI unit of
is the rate at which turbulence kinetic energy is converted into thermal internal energy. The SI unit of  is
is 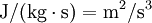 .
.
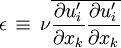
For compressible flows the definition is most often slightly different:
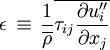
Where the viscous stress, 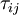 , using Stokes law for mono-atomic gases, is given by:
, using Stokes law for mono-atomic gases, is given by:
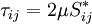
where