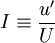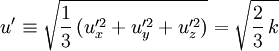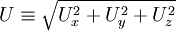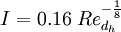Turbulence intensity
From CFD-Wiki
(fixed a typo) |
|||
| (13 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
==Definition== | ==Definition== | ||
| - | The turbulence intensity is defined as: | + | The turbulence intensity, also often refered to as turbulence level, is defined as: |
| - | :<math> | + | :<math>I \equiv \frac{u'}{U}</math> |
Where <math>u'</math> is the root-mean-square of the turbulent velocity fluctuations and <math>U</math> is the mean velocity ([[Reynolds averaging|Reynolds averaged]]). | Where <math>u'</math> is the root-mean-square of the turbulent velocity fluctuations and <math>U</math> is the mean velocity ([[Reynolds averaging|Reynolds averaged]]). | ||
| Line 9: | Line 9: | ||
If the turbulent energy, <math>k</math>, is known <math>u'</math> can be computed as: | If the turbulent energy, <math>k</math>, is known <math>u'</math> can be computed as: | ||
| - | :<math>u' = \sqrt{\frac{2}{3}\, k}</math> | + | :<math>u' \equiv \sqrt{\frac{1}{3} \, ( u_x'^2 + u_y'^2 + u_z'^2 )} = \sqrt{\frac{2}{3}\, k}</math> |
<math>U</math> can be computed from the three mean velocity components <math>U_x</math>, <math>U_y</math> and <math>U_z</math> as: | <math>U</math> can be computed from the three mean velocity components <math>U_x</math>, <math>U_y</math> and <math>U_z</math> as: | ||
| Line 17: | Line 17: | ||
==Estimating the turbulence intensity== | ==Estimating the turbulence intensity== | ||
| - | When setting boundary conditions for a CFD simulation it is often necessary to estimate the turbulence intensity on the inlets. To do this accurately it is | + | When setting boundary conditions for a CFD simulation it is often necessary to estimate the turbulence intensity on the inlets. To do this accurately it is good to have some form of measurements or previous experince to base the estimate on. Here are a few examples of common estimations of the incoming turbulence intensity: |
| - | #'''High-turbulence case''': High-speed flow inside complex geometries like heat- | + | #'''High-turbulence case''': High-speed flow inside complex geometries like heat-exchangers and flow inside rotating machinery (turbines and compressors). Typically the turbulence intensity is between 5% and 20% |
| - | #'''Medium-turbulence case''': Flow in not-so-complex devices like large pipes, ventilation flows etc. or | + | #'''Medium-turbulence case''': Flow in not-so-complex devices like large pipes, ventilation flows etc. or low speed flows (low [[Reynolds number]]). Typically the turbulence intensity is between 1% and 5% |
| - | #'''Low-turbulence case''': Flow originating from a fluid that stands still, like | + | #'''Low-turbulence case''': Flow originating from a fluid that stands still, like external flow across cars, submarines and aircrafts. Very high-quality wind-tunnels can also reach really low turbulence levels. Typically the turbulence intensity is very low, well below 1%. |
| + | |||
| + | ===Fully developed pipe flow=== | ||
| + | |||
| + | For fully developed pipe flow the turbulence intensity at the core can be estimated as: | ||
| + | |||
| + | :<math>I = 0.16 \; Re_{d_h}^{-\frac{1}{8}}</math> | ||
| + | |||
| + | Where <math>Re_{d_h}</math> is the [[Reynolds number]] based on the pipe [[hydraulic diameter]] <math>d_h</math>. | ||
Revision as of 09:14, 3 January 2012
Definition
The turbulence intensity, also often refered to as turbulence level, is defined as:
Where 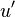 is the root-mean-square of the turbulent velocity fluctuations and
is the root-mean-square of the turbulent velocity fluctuations and 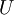 is the mean velocity (Reynolds averaged).
is the mean velocity (Reynolds averaged).
If the turbulent energy, 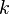 , is known
, is known 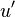 can be computed as:
can be computed as:
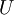 can be computed from the three mean velocity components
can be computed from the three mean velocity components 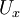 ,
, 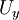 and
and 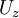 as:
as:
Estimating the turbulence intensity
When setting boundary conditions for a CFD simulation it is often necessary to estimate the turbulence intensity on the inlets. To do this accurately it is good to have some form of measurements or previous experince to base the estimate on. Here are a few examples of common estimations of the incoming turbulence intensity:
- High-turbulence case: High-speed flow inside complex geometries like heat-exchangers and flow inside rotating machinery (turbines and compressors). Typically the turbulence intensity is between 5% and 20%
- Medium-turbulence case: Flow in not-so-complex devices like large pipes, ventilation flows etc. or low speed flows (low Reynolds number). Typically the turbulence intensity is between 1% and 5%
- Low-turbulence case: Flow originating from a fluid that stands still, like external flow across cars, submarines and aircrafts. Very high-quality wind-tunnels can also reach really low turbulence levels. Typically the turbulence intensity is very low, well below 1%.
Fully developed pipe flow
For fully developed pipe flow the turbulence intensity at the core can be estimated as:
Where 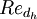 is the Reynolds number based on the pipe hydraulic diameter
is the Reynolds number based on the pipe hydraulic diameter 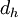 .
.