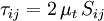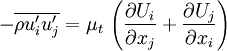Two equation turbulence models
From CFD-Wiki
Two-equation turbulence models are one of the most common type of turbulence models. Models like the k-epsilon model and the k-omega model have become industry standard models and are commonly used for most type of engineering problems. Two-equation turbulence models are also very much still an active area of research and new refined two-equation models are still being developed.
By definition, two-equation models have two extra transport equations to represent the turbulent properties of the flow. Most often one of the transported variables is the turbulent energy,  . The second transported variable can vary depending on what type of two-equation model it is. Common choices are the turbulent dissipation,
. The second transported variable can vary depending on what type of two-equation model it is. Common choices are the turbulent dissipation,  or the specific dissipation,
or the specific dissipation, 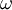 . The second variable can be thought of as the variable that determines the scale of the turbulence (length-scale or time-scale), whereas the first variable,
. The second variable can be thought of as the variable that determines the scale of the turbulence (length-scale or time-scale), whereas the first variable,  , determines the energy in the turbulence.
, determines the energy in the turbulence.
The basis for all two-equation models is the Boussinesq eddy viscosity assumption, which postulates that the Reynolds stress tensor is proportional to the mean strain rate tensor:
Or the same equation written more explicitly: