V2-f models
From CFD-Wiki
(Difference between revisions)
Littleandy (Talk | contribs) m (Category added) |
Littleandy (Talk | contribs) (Short explanation) |
||
| Line 1: | Line 1: | ||
| + | ==Introduction== | ||
| + | The <math>v^2-f</math> model is similar to the [[Standard k-epsilon model]]. Additionally, it incorporates also some near-wall turbulence anisotropy as well as non-local pressure-strain effects. It is a general turbulence model for low [[Reynolds number|Reynolds-numbers]], that does not need to make use of wall functions because it is valid upto solid walls. | ||
| + | The <math>v^2-f</math> model uses a velocity scale, <math>\overline {v^2}</math>, instead of [[turbulent kinetic energy]], <math>k</math>, for the evaluation of the eddy viscosity. <math>\overline {v^2}</math> can be thought of as the velocity fluctuation normal to the streamlines. It can provide the right scaling for the representation of the damping of turbulent transport close to the wall. | ||
| + | |||
| + | ==Limitations== | ||
| + | Can not be used to solve Eulerian multiphase problems. | ||
== References == | == References == | ||
Revision as of 12:09, 4 October 2006
Introduction
The 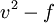 model is similar to the Standard k-epsilon model. Additionally, it incorporates also some near-wall turbulence anisotropy as well as non-local pressure-strain effects. It is a general turbulence model for low Reynolds-numbers, that does not need to make use of wall functions because it is valid upto solid walls.
The
model is similar to the Standard k-epsilon model. Additionally, it incorporates also some near-wall turbulence anisotropy as well as non-local pressure-strain effects. It is a general turbulence model for low Reynolds-numbers, that does not need to make use of wall functions because it is valid upto solid walls.
The 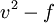 model uses a velocity scale,
model uses a velocity scale, 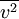 , instead of turbulent kinetic energy,
, instead of turbulent kinetic energy,  , for the evaluation of the eddy viscosity.
, for the evaluation of the eddy viscosity. 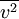 can be thought of as the velocity fluctuation normal to the streamlines. It can provide the right scaling for the representation of the damping of turbulent transport close to the wall.
can be thought of as the velocity fluctuation normal to the streamlines. It can provide the right scaling for the representation of the damping of turbulent transport close to the wall.
Limitations
Can not be used to solve Eulerian multiphase problems.
References
- Durbin, P. Separated flow computations with the
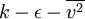 model, AIAA Journal, 33, 659-664, 1995.
model, AIAA Journal, 33, 659-664, 1995.
