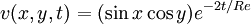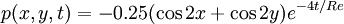Viscous diffusion of multiple vortex system
From CFD-Wiki
(Difference between revisions)
| Line 1: | Line 1: | ||
| - | The following analytical solution satisfies the incompressible continuity and momentum | + | The following analytical solution satisfies the viscous, incompressible |
| - | equations in dimension-less form in the domain <math>0 \le x, y \le 2\pi</math>. The | + | continuity and momentum equations in dimension-less form in the domain <math>0 |
| - | solution is periodic in both <math>x</math> and <math>y</math> coordinates. | + | \le x, y \le 2\pi</math>. The solution is periodic in both <math>x</math> and |
| + | <math>y</math> coordinates. | ||
:<math> | :<math> | ||
| - | u(x,y,t) = -\cos x \sin y e^{-2t/Re} | + | u(x,y,t) = -(\cos x \sin y) e^{-2t/Re} |
</math> | </math> | ||
:<math> | :<math> | ||
| - | v(x,y,t) = \sin x \cos y e^{-2t/Re} | + | v(x,y,t) = (\sin x \cos y) e^{-2t/Re} |
</math> | </math> | ||
| Line 14: | Line 15: | ||
p(x,y,t) = -0.25( \cos 2x + \cos 2y) e^{-4t/Re} | p(x,y,t) = -0.25( \cos 2x + \cos 2y) e^{-4t/Re} | ||
</math> | </math> | ||
| + | |||
| + | where <math>u,v</math> are the Cartesian velocity components, <math>p</math> | ||
| + | is the pressure and <math>Re</math> is the [[Reynolds number]]. | ||
Revision as of 08:26, 16 September 2005
The following analytical solution satisfies the viscous, incompressible
continuity and momentum equations in dimension-less form in the domain 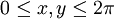 . The solution is periodic in both
. The solution is periodic in both 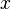 and
and
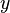 coordinates.
coordinates.
where 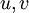 are the Cartesian velocity components,
are the Cartesian velocity components, 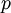 is the pressure and
is the pressure and 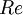 is the Reynolds number.
is the Reynolds number.