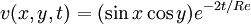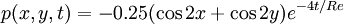Viscous diffusion of multiple vortex system
From CFD-Wiki
(Difference between revisions)
m |
|||
| Line 13: | Line 13: | ||
:<math> | :<math> | ||
| - | p(x,y,t) = -0.25( \cos 2x | + | p(x,y,t) = -0.25( \cos 2x + \cos 2y) e^{-4t/Re} |
</math> | </math> | ||
where <math>u,v</math> are the Cartesian velocity components, <math>p</math> | where <math>u,v</math> are the Cartesian velocity components, <math>p</math> | ||
is the pressure and <math>Re</math> is the [[Reynolds number]]. | is the pressure and <math>Re</math> is the [[Reynolds number]]. | ||
Latest revision as of 07:40, 12 April 2007
The following analytical solution satisfies the viscous, incompressible
continuity and momentum equations in dimension-less form in the domain 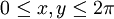 . The solution is periodic in both
. The solution is periodic in both 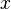 and
and
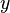 coordinates.
coordinates.
where 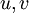 are the Cartesian velocity components,
are the Cartesian velocity components, 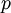 is the pressure and
is the pressure and 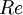 is the Reynolds number.
is the Reynolds number.