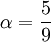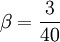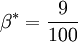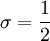Wilcox's k-omega model
From CFD-Wiki
(Difference between revisions)
(→Closure Coefficients and Auxilary Relations) |
Malkavian GT (Talk | contribs) m (→References) |
||
| (13 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
| + | {{Turbulence modeling}} | ||
==Kinematic Eddy Viscosity == | ==Kinematic Eddy Viscosity == | ||
:<math> | :<math> | ||
| Line 15: | Line 16: | ||
==Closure Coefficients and Auxilary Relations== | ==Closure Coefficients and Auxilary Relations== | ||
| + | |||
:<math> | :<math> | ||
\alpha = {{5} \over {9}} | \alpha = {{5} \over {9}} | ||
| Line 41: | Line 43: | ||
== References == | == References == | ||
| - | #{{reference- | + | #{{reference-paper|author=Wilcox, D.C. |year=1988|title=Re-assessment of the scale-determining equation for advanced turbulence models|rest=AIAA Journal, vol. 26, no. 11, pp. 1299-1310}} |
| + | |||
| + | [[Category:Turbulence models]] | ||
Latest revision as of 16:52, 8 March 2011
Contents |
Kinematic Eddy Viscosity
Turbulence Kinetic Energy
Specific Dissipation Rate
Closure Coefficients and Auxilary Relations
References
- Wilcox, D.C. (1988), "Re-assessment of the scale-determining equation for advanced turbulence models", AIAA Journal, vol. 26, no. 11, pp. 1299-1310.

 model
model
 model
model
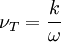
![{{\partial k} \over {\partial t}} + U_j {{\partial k} \over {\partial x_j }} = \tau _{ij} {{\partial U_i } \over {\partial x_j }} - \beta ^* k\omega + {\partial \over {\partial x_j }}\left[ {\left( {\nu + \sigma ^* \nu _T } \right){{\partial k} \over {\partial x_j }}} \right]](/W/images/math/1/a/4/1a436edcf81f2ccbdf53dfa7dd9e0550.png)
![{{\partial \omega } \over {\partial t}} + U_j {{\partial \omega } \over {\partial x_j }} = \alpha {\omega \over k}\tau _{ij} {{\partial U_i } \over {\partial x_j }} - \beta \omega ^2 + {\partial \over {\partial x_j }}\left[ {\left( {\nu + \sigma \nu _T } \right){{\partial \omega } \over {\partial x_j }}} \right]](/W/images/math/b/3/6/b361dbe1c46fcbcbf1795a2997a00e09.png)