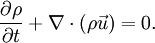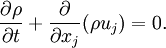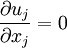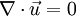Continuity equation
From CFD-Wiki
(Redirected from Continuity Equation)
In fluid dynamics, the continuity equation is an expression of conservation of mass. In (vector) differential form, it is written as
where 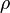 is density,
is density, 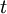 is time, and
is time, and 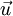 is fluid velocity. In cartesian tensor notation, it is written as
is fluid velocity. In cartesian tensor notation, it is written as
For incompressible flow, the density drops out, and the resulting equation is
in tensor form or
in vector form. The left-hand side is the divergence of velocity, and it is sometimes said that an incompressible flow is divergence free.