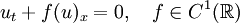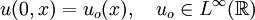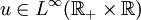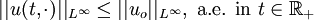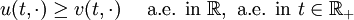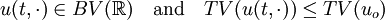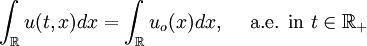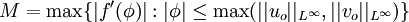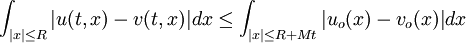Kruzkov theorem
From CFD-Wiki
The scalar Cauchy problem
with initial condition
has a unique entropy solution
which fulfills (important for numerics)
- Stability
- Monotone solution: If
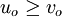 a.e. in
a.e. in 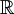 then
then
- TV-diminishing: If
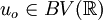 then
then
- Conservation: If
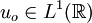 then
then
- Finite domain of dependence: If
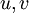 are two entropy solutions, corresponding to initial conditions
are two entropy solutions, corresponding to initial conditions 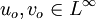 and
and
then