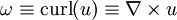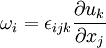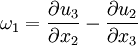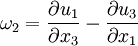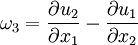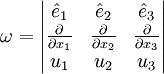Vorticity
From CFD-Wiki
Vorticity is a vector field variable which is derived from the velocity vector. Mathematically, it is defined as the curl of the velocity vector
In tensor notation, vorticity is given by:
where 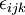 is the alternating tensor. The components of vorticity in Cartesian coordinates are;:
is the alternating tensor. The components of vorticity in Cartesian coordinates are;:
This can be obtained by using determinants
where 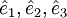 are the unit vectors for the Cartesian coordinate system.
are the unit vectors for the Cartesian coordinate system.
Physical Significance
The vorticity can be seen as a vector having magnitude equal to the maximum "circulation" at each point and to be oriented perpendicularly to this plane of circulation for each point.