A note for CFD developers and the Spalart-Allmaras model
This is a pretty specific issue which relates to my experience working on wall functions and the Spalart-Allmaras model, but might be useful to others or, more importantly, the users of their code.
If you followed my previous posts here, you know I developed a wall function formulation based on the Musker wall function which, thanks to a math trick, is integrable also for arbitrary Pr/Pr_t (Sc/Sc_t) numbers and also for some forms of non equilibrium terms.
One of the nice things about this formulation is that it uses the same form of turbulent viscosity approximation that holds for the Spalart-Allmaras model near a wall, as they both use:

where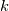 is the Von Karman constant and
is the Von Karman constant and  is the
is the 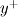 value where
value where 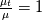 . The formulation implies
. The formulation implies 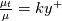 for large
for large 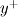 and
and 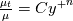 near the wall, with:
near the wall, with:
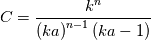
The classical Musker formulation uses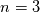 , which is the correct near wall behavior, while the SA model uses instead
, which is the correct near wall behavior, while the SA model uses instead 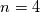 , which was claimed to be ininfluent in the original paper, yet certainly uncorrect. Also, the constant implied by the SA model is given by:
, which was claimed to be ininfluent in the original paper, yet certainly uncorrect. Also, the constant implied by the SA model is given by:
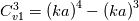
which for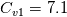 gives, approximately,
gives, approximately, 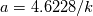 (but could be also expressed in closed form for arbitrary
(but could be also expressed in closed form for arbitrary 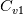 ).
).
Besides the near wall behavior, a striking difference between the SA near wall behavior and the Musker one is that latter is easily integrable to a nice closed form wall function and, as I have shown in previous posts, the same holds for the temperature and other scalars. While the same is formally true also for the SA model, as shown here:
https://www.iccfd.org/iccfd7/assets/...1902_paper.pdf
it is debatable that the "nice" and "closed" form description applies to that as well; also, it is unclear if the approach can be extended to temperature and scalars. Nonetheless, the above SA wall function has already found widespread use, at least in academic applications.
This note comes from the desire and attempt to modify the SA model in a well known CFD code that, indeed, allows the user to implement their own turbulent viscosity formulation. The idea was to force the SA model to behave at wall as the Musker wall function.
Indeed, the SA model is built in such a way that, in cases where wall functions conditions apply (i.e.,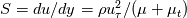 ), the prescribed
), the prescribed 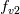 formula, independently from how
formula, independently from how  is defined, allows the linear solution
is defined, allows the linear solution 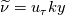 to hold in the whole viscous+buffer+log zone. That is, under the classical equilibrium assumptions, a proper
to hold in the whole viscous+buffer+log zone. That is, under the classical equilibrium assumptions, a proper 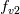 should ensure that the SA solution is always of the following form, independently from
should ensure that the SA solution is always of the following form, independently from  :
:
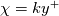
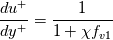
This preliminary examination then suggests that the Musker behavior could be reached by simply using:
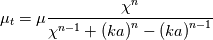
with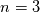 , where:
, where:
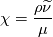
However, this was not possible as the code was hardcoded to use:
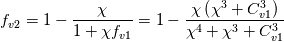
in the production and destruction terms, instead of:
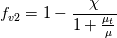
So, in order to apply the correct modification, an additional source term has to be supplied, that deletes the old production and destruction and uses the new ones. This, of course, is just as cumbersome as it sounds, and requires some insight into the SA model that a typical user wouldn't probably have (not even myself, considering that the first implementations of this approach didn't recognize the need to alter also the destruction term).
In conclusion, the present note is to suggest that implementations of the SA model should use the following definition of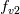 :
:
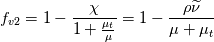
which makes it valid for whatever definition of the turbulent viscosity. The immediate gain is that now one can easily implement a SA version with the correct near wall behavior and simple, all-y+, analytical wall function.
In the end, the implementation used in the attached source code here worked much better than the one only affecting the turbulent viscosity.
Still, the match is not as perfect as when one compares the original SA with its underlying wall function. In particular, for some reason, the turbulent viscosity ratio fails to reach exactly 1 at the exact prescribed location (a=11.0409) and there is a slight bump in the otherwise linear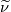 behavior.
behavior.
Note that for a closed source tool like the one used in this test, the exercise above is basically cherry-picking until you get all the terms right (as it is impossible to know which terms were implemented using the turbulent viscosity and which ones using ). So, this must be considered just as an exercise or, at best, a work in progress. The very point here is, a correct implementation is independent from
). So, this must be considered just as an exercise or, at best, a work in progress. The very point here is, a correct implementation is independent from  .
.
OpenFOAM, for example, seems to be correctly implemented, so that one should really just modify the definition of in SpalartAllmaras.C and is ready to go.
in SpalartAllmaras.C and is ready to go.
If you followed my previous posts here, you know I developed a wall function formulation based on the Musker wall function which, thanks to a math trick, is integrable also for arbitrary Pr/Pr_t (Sc/Sc_t) numbers and also for some forms of non equilibrium terms.
One of the nice things about this formulation is that it uses the same form of turbulent viscosity approximation that holds for the Spalart-Allmaras model near a wall, as they both use:

where
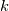 is the Von Karman constant and
is the Von Karman constant and  is the
is the 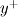 value where
value where 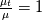 . The formulation implies
. The formulation implies 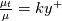 for large
for large 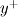 and
and 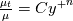 near the wall, with:
near the wall, with: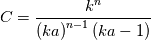
The classical Musker formulation uses
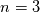 , which is the correct near wall behavior, while the SA model uses instead
, which is the correct near wall behavior, while the SA model uses instead 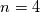 , which was claimed to be ininfluent in the original paper, yet certainly uncorrect. Also, the constant implied by the SA model is given by:
, which was claimed to be ininfluent in the original paper, yet certainly uncorrect. Also, the constant implied by the SA model is given by: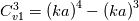
which for
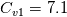 gives, approximately,
gives, approximately, 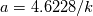 (but could be also expressed in closed form for arbitrary
(but could be also expressed in closed form for arbitrary 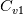 ).
).Besides the near wall behavior, a striking difference between the SA near wall behavior and the Musker one is that latter is easily integrable to a nice closed form wall function and, as I have shown in previous posts, the same holds for the temperature and other scalars. While the same is formally true also for the SA model, as shown here:
https://www.iccfd.org/iccfd7/assets/...1902_paper.pdf
it is debatable that the "nice" and "closed" form description applies to that as well; also, it is unclear if the approach can be extended to temperature and scalars. Nonetheless, the above SA wall function has already found widespread use, at least in academic applications.
This note comes from the desire and attempt to modify the SA model in a well known CFD code that, indeed, allows the user to implement their own turbulent viscosity formulation. The idea was to force the SA model to behave at wall as the Musker wall function.
Indeed, the SA model is built in such a way that, in cases where wall functions conditions apply (i.e.,
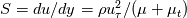 ), the prescribed
), the prescribed 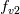 formula, independently from how
formula, independently from how  is defined, allows the linear solution
is defined, allows the linear solution 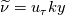 to hold in the whole viscous+buffer+log zone. That is, under the classical equilibrium assumptions, a proper
to hold in the whole viscous+buffer+log zone. That is, under the classical equilibrium assumptions, a proper 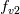 should ensure that the SA solution is always of the following form, independently from
should ensure that the SA solution is always of the following form, independently from  :
: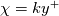
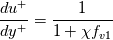
This preliminary examination then suggests that the Musker behavior could be reached by simply using:
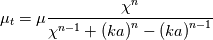
with
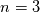 , where:
, where: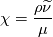
However, this was not possible as the code was hardcoded to use:
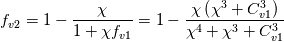
in the production and destruction terms, instead of:
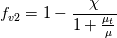
So, in order to apply the correct modification, an additional source term has to be supplied, that deletes the old production and destruction and uses the new ones. This, of course, is just as cumbersome as it sounds, and requires some insight into the SA model that a typical user wouldn't probably have (not even myself, considering that the first implementations of this approach didn't recognize the need to alter also the destruction term).
In conclusion, the present note is to suggest that implementations of the SA model should use the following definition of
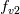 :
: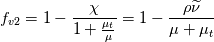
which makes it valid for whatever definition of the turbulent viscosity. The immediate gain is that now one can easily implement a SA version with the correct near wall behavior and simple, all-y+, analytical wall function.
In the end, the implementation used in the attached source code here worked much better than the one only affecting the turbulent viscosity.
Still, the match is not as perfect as when one compares the original SA with its underlying wall function. In particular, for some reason, the turbulent viscosity ratio fails to reach exactly 1 at the exact prescribed location (a=11.0409) and there is a slight bump in the otherwise linear
 behavior.
behavior.Note that for a closed source tool like the one used in this test, the exercise above is basically cherry-picking until you get all the terms right (as it is impossible to know which terms were implemented using the turbulent viscosity and which ones using
 ). So, this must be considered just as an exercise or, at best, a work in progress. The very point here is, a correct implementation is independent from
). So, this must be considered just as an exercise or, at best, a work in progress. The very point here is, a correct implementation is independent from  .
.OpenFOAM, for example, seems to be correctly implemented, so that one should really just modify the definition of
 in SpalartAllmaras.C and is ready to go.
in SpalartAllmaras.C and is ready to go.Total Comments 0





