(??) sinusoidal motion for DEFINE_CG_MOTION
 

I'm testing with a simple UDF for sinusoidal angular velocity motion but it has a problem.

macro [DEFINE_CG_MOTION] presents [omega] for angular velocity variable and [time] to passes time variable, so try this to describe a pseudo-vibrating cantilever.

omega is time dependant variable and displacement(angle) is intergation of the omega over the time passed. so I assumed if I put some intergand of the time into UDF, Fluent will reflect its integration to the moving boundary.

Few graphs were ploted for investigation

http://yfrog.com/51graphbj(http://yfrog.com/51graphbj)

and equations are...

w_1=sin(2*pi*t)
F_1 = INTEGRAL(w_1, t)

w_2=sin(2*pi*t + pi/2)
F_2 = INTEGRAL(w_2, t)

w_3=sin(2*pi*t - pi/2)
F_3 = INTEGRAL(w_3, t)

I choosed blue one(w_2) and its UDF code were...

DEFINE_CG_MOTION(move, dt, vel, omega, time, dtime)
{
NV_S(vel, =, 0.0);
NV_S(omega, =, 0.0);
omega[2]=sin(2*M_PI*time + M_PI/2);
}


my desired output was correct y position of lever though, it only moves over y=0 but y>0 and vise versa (no alternation of -+. just up and down under y=0 or over y=0).

I have no idea for [dtime] and [accumulater+= valiable] form to the that situation. So I put integrand in the UDF and hope the Fluent updates position of that intergrand for the time, but it seemed not that explictly :(

SO... It seems obiously there are stupid assumption or mis-understanding of UDF. Can I recieve a wise solution?

First of all, I don't see why F_1 is always positive in your picture (http://yfrog.com/51graphbj).
If angular velocity is:
1.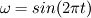
then the integral of it should be: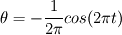

which alternates between
2.
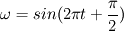then the integral of it should be: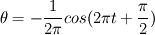

which again alternates between

My suggestion is to check around which origing you define this omega!