
 |
Adding a source term in k-epsilon model
Hi all,
I am testing out a model raised by S.B. Pope, which modified the epsilon equation with a source term. I tried to implement it with udf in the FLUENT, but the convergence seems to be a problem. The modified epsilon-equation looks like the following: ![{\displaystyle {\frac {\partial (\rho \epsilon )}{\partial t}}+{\frac {\partial (\rho \epsilon u_{i})}{\partial x_{i}}}={\frac {\partial }{\partial x_{j}}}\left[{\frac {\mu _{t}}{\sigma _{\epsilon }}}{\frac {\partial \epsilon }{\partial x_{j}}}\right]+C_{1\epsilon }{\frac {\epsilon }{k}}2{\mu _{t}}{E_{ij}}{E_{ij}}-(C_{2\epsilon }-C_{3\epsilon}\chi)\rho {\frac {\epsilon ^{2}}{k}}} {\displaystyle {\frac {\partial (\rho \epsilon )}{\partial t}}+{\frac {\partial (\rho \epsilon u_{i})}{\partial x_{i}}}={\frac {\partial }{\partial x_{j}}}\left[{\frac {\mu _{t}}{\sigma _{\epsilon }}}{\frac {\partial \epsilon }{\partial x_{j}}}\right]+C_{1\epsilon }{\frac {\epsilon }{k}}2{\mu _{t}}{E_{ij}}{E_{ij}}-(C_{2\epsilon }-C_{3\epsilon}\chi)\rho {\frac {\epsilon ^{2}}{k}}}](/Forums/vbLatex/img/6d5bb62191cc7504af7430441e550a3a-1.gif) The added source term is related to the  term, which is a measure of the vortex stretching. Here, term, which is a measure of the vortex stretching. Here, 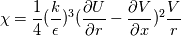 . .The case I am simulating is basically a turbulent round jet. I firstly calculated the case until convergence, and then implemented the source term to the epsilon equation as the following code: Code:
#include "udf.h"https://image.ibb.co/f30FH0/1234.png Clearly the white line (continuity) is driven to a very high level. Also other variables would not converge. Interestingly if I do not initiate with the calculation of the standard model, the residual stabilizes at a even higher value. Cannot figure out what is going wrong. I tried to observe the flow field, and find out that the v,k,epsilon fields are all making no sense. I think the problem comes with the udf and I might have not done it properly. What I am doing is simply to add the 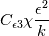 term as the source term directly. What is the issue with that? term as the source term directly. What is the issue with that?Thanks so much for your help! |
Hi cshsgy, did you solve the issue? I plan to do a similar implementation.
|
| All times are GMT -4. The time now is 22:51. |