
 |
Pressure correction in fractional step method
Can someone explain to me how the pressure correction step works in cylindrical coordinates? I have been working on a code for a while and my pressure correction step is not producing a divergence free field.
|
Quote:
|
How does the divergence change before and after the correction step?
Is the divergence localized in certain regions after the correction step? How accurately is your pressure equation being solved? Are you using an axisymmetric cylindrical grid, is weird stuff happening at the axis of symmetry? |
Quote:
Quote:
I initially start with a velocity profile of 1 everywhere in the field. When integrated it produces a value of 1. I expect that at any time, if I integrate the velocity profile, I should also get a value of 1. However as my flow progresses to steady state, I get values up to 1.2 |
Are you using an exact or approximate projection method?
You must be careful in the inner-outer product of discretized divergence-gradient operators |
|
The pressure equation must be discretized from the Div Grad (*) operators, you should not use the Laplace operator. This allows you to substitute the correct BC in terms of the normal component of the pressure gradient
|
Quote:
|
Also are there any books or papers that I can look up that talk about how to do this?
|
for those interested, I found this paper which essentially talks about my problem. Unfortunately I still have not found the bug in my code. I expect my code to produce a poiseuielle like profile that peaks at 1.5 however my code peaks at ~1.8 and is not divergence free.
If anyone has seen similar problems, please let me know. thanks http://www.sciencedirect.com/science...45793004001148 |
Quote:
|
Quote:
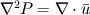 I didn't put in the time because it cancels once applied in the navier stokes equations. Quote:
|
is not a problem if you then compute
Vn+1= V* - Grad P In any case, I am quite sure you have problems in setting pressure BCs ... you must write Div (Grad P) and substitute n.Grad P at boundaries |
I think I have accounted for that. Since my code is on a staggered grid, I'm only calculating pressure at the interior points. At the edges, I assume that the ghost point outside the boundary is the same as the first interior point. For example the second derivative in the R direction should be
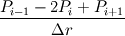 . Substituting for neumann bcs I get . Substituting for neumann bcs I get 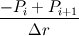 at the axis and at the axis and 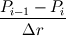 at the wall. at the wall. |
Quote:
I do not have time right now to figure this out. But I will try to imbibe what you wrote. I am assuming the P in your equation is pressure correction and not the pressure itself. I asked that because I never remember deriving pressure correction in fractional step method that is independent of delta T. |
Quote:
You can not apply zero gradient at the axis by ghost points. Axis has pressure gradients. Quote:
|
There normal component of the gradient of the pressure should be zero at the axis, if we are assuming axisymmetric flow and the fact that Ur must be zero at the axis.
What are you using for the inlet/oulet conditions? |
Quote:
If anyone is interested or if anyone thinks seeing the code might help, then i can post my matlab code. I'm pretty sure that this poisson equation solver is the last bug in my code. |
I think I figured out where the error is. When I formulate the finite difference matrix for the laplacian, I essentially solve Ax = b. However A is nearly singular and so my solution ends up being innacurate. How can I increase the accuracy?
|
| All times are GMT -4. The time now is 01:59. |