| jojo81 |
October 15, 2012 12:05 |
Analytic solution for 2D steady Euler equations
Hello,
I'm trying to verifiy my CFD code for low Mach number flows with some analytical or manufactured solutions.
The convection and/or diffusion equation for a scalar is fine and now I focus on the Navier Stokes equations:
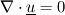
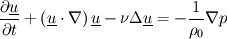
First, I want to check the non linear convection term, so I suppress the viscosity considering a perfect fluid and starting from the Green Taylor vorticies solution for Navier Stokes:
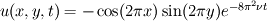
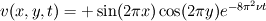
![p(x,y,t) = -\frac{1}{4}\left[\cos(4 \pi x) + \cos (4 \pi y)\right] e^{- 16 \pi^2 \nu t} p(x,y,t) = -\frac{1}{4}\left[\cos(4 \pi x) + \cos (4 \pi y)\right] e^{- 16 \pi^2 \nu t}](/Forums/vbLatex/img/f6c2d5e118601cbdfceedd8cfe9c1749-1.gif)
I get this solution:
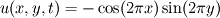

![p(x,y,t) = -\frac{1}{4}\left[\cos(4 \pi x) + \cos (4 \pi y)\right] p(x,y,t) = -\frac{1}{4}\left[\cos(4 \pi x) + \cos (4 \pi y)\right]](/Forums/vbLatex/img/4bcc55b399cf9520ce91cca222262640-1.gif)
which satisfies the steady Euler equations:
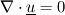
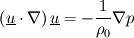
I tried this solution with my CFD code setting boundary and initial conditions with the solution, the pressure is also imposed, not computed, with the solution.
At each iteration, I solve the velocity components and then update the convective flux, solve velocity, update the convective flux, etc. I use finite volume, upwind or centered convective scheme.
My problem: after some oscillations, the flow diverges and I don't understand why. Is the solution unstable ? Can't a solver for Navier Stokes solve an Euler problem ?
Did or is anybody try this kind of problem ?
Thanks. |

