CFD Online Discussion Forums - Turbulence model parameters and equations

Dear CFD users,

Right now I´m working on a CFD computation for external flow around a very streamlined car.
I have some questions regarding the turbulence parameters. I´ll first specify what formulas I used to calculate some parameters. FYI, I use FineOpen of Numeca. I will either use the SA or Mentor-SST k –omega (Extended wall) model.

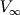
Description of the stream: A free steam around a car driving in the open i.e. on the road. So it is an external flow. The free stream velocity $V_{\infty}$ is 25 m/s.

There are a couple parameters I have to specify in the CFD software program which im not complete sure about, being:

Boundary conditions:
for the k-omega model: k and $\varepsilon$
for the Spalart-Allmaras model: turbulent viscosity

Initial conditions:
for the k-omega model: k and $\varepsilon$
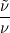
for the Spalart-Allmaras model: ratio $\frac{\tilde{\nu}}{\nu}$ (taken as 1)
So it comes down to calculating/guestimating these parameters. I used the following formulas (all in SI units) to calculate these parameters:

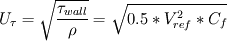
$U_{\tau}=\sqrt{\frac{\tau_{wall}}{\rho}}=\sqrt{0.5*V_{ref}^2*C_f}$ (From Numeca FineOpen manual)
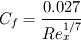
$C_f=\frac{0.027}{Re_x^{1/7}}$ (Also from FineOpen manual)
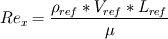
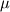
$Re_x=\frac{\rho_{ref}*V_{ref}*L_{ref}}{\mu}$ with $\mu$ being the dynamic (molecular) viscosity
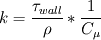
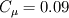
$k=\frac{\tau_{wall}}{\rho}*\frac{1}{C_{\mu}}$ with $C_{\mu}=0.09$ and $\frac{\tau_{wall}}{\rho}=0.5*V_{ref}^2*C_f$
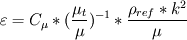
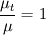
$\varepsilon=C_{\mu}*(\frac{\mu_t}{\mu})^{-1}*\frac{\rho_{ref}*k^2}{\mu}$ I took $\frac{\mu_t}{\mu}=1$ (Numeca specifies in the manual that a typical value for this ratio is 1 for external flows). So before I can calculate $\varepsilon$ , I first calculate k.

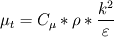
Turbulent (eddy) viscosity $\mu_t=C_{\mu}*\rho*\frac{k^2}{\varepsilon}$ (So before calculating this parameter, I first calculate k, then $\varepsilon$ and then $\mu_t$ )

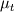
Using the above mentioned formulas, I was able to calculate all the needed parameters. Still I’m not sure if these formulas are correct or maybe are not valid in every case.

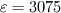
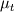
However, when I just assume these formulas are correct I calculated k, $\varepsilon=3075$ and $\mu_t$ . This yielded
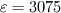
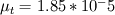
k = 0.718, $\varepsilon=3075$ and $\mu_t=1.85*10^-5$ . Do these values make sense in anyway, or are they completely out of range?

The actual reason I’m posting this question is to validate our computation. One year ago, a group performed the same computation for the exact same car. This yielded a drag force of about 40N. The problem we are having now is that the drag force is in the order of 10^4 Newton. Obviously this does not make sense. Right now the mesh I runned in FineOpen contains about 18 million cells with refinements near the car itself, behind the car, beneath the car etc. etc.

So what I’m specifically asking:
1) Can someone verify the method I use, especially the formulas I use
2) What may cause the problem of a way too high drag value?
3) Do the values of k and epsilon make sense?

I know these are a lot of questions, but any help is much appreciated.
Thank you in advance,

Maximus