 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Member
Dokeun, Hwang
Join Date: Apr 2010
Location: Korea, Republic of
Posts: 98
Rep Power: 16  |
Hello
From J.Blazek's, intercell flux for roe is expressed as a production of roe matrix and difference of conservation variables between left & right So, I'm trying to derive eigenvalues, eigenvectors, wave strength from roe matrix written for 2D Euler Finite volume scheme. But I confused whether I'm doing right. Many references explain the conservation lows and roe flux in serperated coordinates. From Toro, there is a method to express these flux terms as one augmented 1D flux. Where can I find a whole process to derive roe matrix for the augmented 1D flux!? Any kind of advice will be a help. Thank you in advance. |
|
|
|

|
|
|
|
|
#2 |
|
New Member
Vasiliy
Join Date: Feb 2011
Posts: 9
Rep Power: 15  |
Try to find Weiss and Smith paper "Preconditioning Applied to Variable and Constant Density Time-Accurate Flows on Unstructured Meshes".
May by it can be useful for you. |
|
|
|

|
|
|
|
|
#3 | |
|
Member
Jack
Join Date: Dec 2011
Posts: 94
Rep Power: 14  |
Quote:
To find more details about Roe scheme, the chapter 11 from "Riemann Solvers and Numerical Methods for Fluid Dynamics A Practical Introduction" by Toro, E. F. will be very helpful! |
||
|
|

|
||
|
|
|
#4 |
|
Member
Dokeun, Hwang
Join Date: Apr 2010
Location: Korea, Republic of
Posts: 98
Rep Power: 16  |
Dear Vasiliy, ripperjack
Thank you for your advices. I just read the paper and the took. But I think they didn't resolve my concern. Maybe I didn't describe the exact point I stuck. So, I'd like to change my question. The discretized integral form of conservation laws(2d euler) for unstructured scheme is 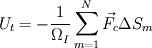 . . In order to find inter cell flux by roe shceme, I needed to fined 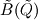 and and 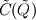 which satisfy following relations, which satisfy following relations,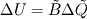 , , 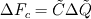 , , Paramether vector 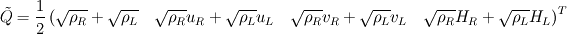 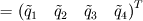 , ,And 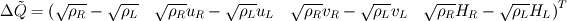 from these I can find roe matrix 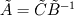 . .But, the problem is that it's too complicate to find 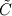 from flux from flux 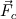 . .Here, 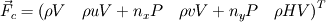 . .I'd like to know that obtaining  from above relation is straightforward despite of its complexity. from above relation is straightforward despite of its complexity.For the 1st row of 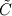 , I found , I found 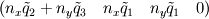 but I couldn't for the other rows. It's too complicated. but I couldn't for the other rows. It's too complicated.If the fluxs are splitted x, y direction(structured scheme) I have no problem with it. I'd like to know if I'm going a right way.  Thank you. |
|
|
|

|
|
|
|
|
#5 |
|
Member
Jack
Join Date: Dec 2011
Posts: 94
Rep Power: 14  |
Quote:
It seems that you are trying to derive Roe matrix  , and calculate the flux at the cell surfaces. , and calculate the flux at the cell surfaces. I did not know the details of derivation of Roe matrix 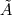 , I just used it. , I just used it. And 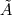 is exact the same as the original convective Jacobian A in 2D Euler equation, except that the flow variables are replaced with the Roe averaged variables (see J.Blazek's book, p108). is exact the same as the original convective Jacobian A in 2D Euler equation, except that the flow variables are replaced with the Roe averaged variables (see J.Blazek's book, p108). And the flux at the cell surface can be calculate by: 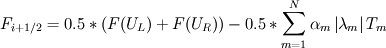 The 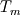 is the mth right eigenvector based on the Roe averaged matrix is the mth right eigenvector based on the Roe averaged matrix 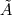 , , 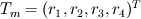 The 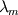 is the mth eigenvalue also based on the is the mth eigenvalue also based on the 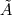 The wave strength 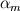 is defined by: is defined by: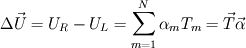 so the wave strength 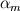 can be calculated by: can be calculated by: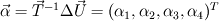 and 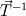 is the left eigenvector based on the is the left eigenvector based on the 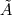 The left and right eigenvector can be find in J.Blazek's book A.11 In addition, if you just want to use Roe scheme, the Eq. 4.91-4.95 in J.Blazek's book can be used directly. I used that equations and they worked good. That is all I can do, hope that would help! 
|
|
|
|

|
|
|
|
|
#6 |
|
New Member
Join Date: Jan 2012
Posts: 9
Rep Power: 14  |
You mentioned the Matrix T of the right eigenvectors and the book of Blazek.
There's a big question that bothers me for years: Did somebody realize that in some components of the Matrix T in Blazek's book (formula A. 66, p. 426, 1st ed. 2001) the units are non consistent? I mean in the first three columns, rows 2 to 4, there are matrix-entries like 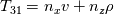 How can a quantity of units [velocity] be added to a quantity of units [density]? The same question applies to the book of Hirsch (vol. 2, formula (16.5.22), p. 181), which shows basically the same T-matrix (it's called P there and scaled by factor 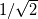 ). By the way, Hirsch is the only source where substeps for the derivation are given in addition to the resulting eigenvector matrices. Does anybody know another place where the derivation of the eigenvectors is explained step by step? ). By the way, Hirsch is the only source where substeps for the derivation are given in addition to the resulting eigenvector matrices. Does anybody know another place where the derivation of the eigenvectors is explained step by step?
Last edited by koderer; March 2, 2018 at 17:52. |
|
|
|

|
|
|
|
|
#7 |
|
Senior Member
|
The very point on eigenvectors is that they are not uniquely determined, so different results can be obtained. The one I like more is:
Balasubramanian, Chen: Preconditioned Algorithms with a General Equation of State for Rotating Machinery Flows, AIAA 2010-4862. EDIT: I don't have confidence with those formulations showing inconsistencies, so I cannot give help on that. |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| On the damBreak4phaseFine cases | paean | OpenFOAM Running, Solving & CFD | 0 | November 14, 2008 21:14 |
| Roe scheme for general equation of state | zouchu | Main CFD Forum | 3 | August 10, 2000 16:46 |
| roe scheme | Jian Xia | Main CFD Forum | 7 | August 9, 2000 01:18 |
| Roe FDS scheme applied to backward facing | Mohammad Kermani | Main CFD Forum | 6 | December 29, 1999 11:11 |
| Roe Scheme; Shock Boundary layer Interaction | Mohammad Kermani | Main CFD Forum | 5 | December 20, 1999 15:44 |