 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Join Date: Apr 2013
Posts: 15
Rep Power: 13  |
Hi all,
I want to see the orthogonality of the chebyshev polynomials in Matlab. The nodes I choose is the Chebyshev nodes, 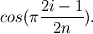 . i=1.....n . i=1.....nAccording to the approximation theory, I can have 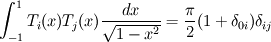 Now, how can I numerically show that the orthogonality? What I did is (1) I generate the chebyshev polynomials in Matlab, stored in p(:,i), i is the order 0....n (2) sum(p(:,i).*p(:,j)), meaning that the component-wise sum of the i-th order chebyshev and j-th one. But it turns out that some of the results work, some of them don't. Did I do something wrong here? I didn't mention the weight function since for the chebyshev nodes, the weight function is constant pi/n. So at least, it should affect the orthogonality. Any comments? Thanks. |
|
|
|

|
|
|
|
|
#2 |
|
New Member
Join Date: Apr 2013
Posts: 15
Rep Power: 13  |
Sorry, please ignore this thread. Problem solved.
|
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Chebyshev collocation method | Sun Yuhui | Main CFD Forum | 3 | May 6, 2012 02:46 |
| 2D pseudo-spectral (Chebyshev) parallel Helmholtz solver package | magicsquirrel | Main CFD Forum | 0 | July 13, 2011 10:45 |
| nasa polynomials | gardian | CFX | 3 | March 10, 2011 06:29 |
| Chebyshev Polynomials in a infinite Channel??? | Carlos | Main CFD Forum | 5 | April 9, 2002 15:05 |
| Chebyshev grid | Annie | Main CFD Forum | 4 | February 11, 2002 07:00 |