 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Member
M. Nabi
Join Date: Jun 2009
Posts: 44
Rep Power: 16  |
Hi all,
I am writing a code for LES. This code is based on a structured curvilinear grids with strong stretching beside the walls. In order to reduce the restrictions for time step, I used Adams-Bashforth for the convection term and Crank-Nicholson for the diffusion term. ![\frac{\partial}{\partial x_j} \left[ \left( \nu + \nu_t \right) \left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i} \right) \right]
=
\frac{\partial}{\partial x_j} \left[ \left( \nu + \nu_t \right) \left( \frac{\partial u_i}{\partial x_j} \right) \right]
+
\frac{\partial}{\partial x_j} \left[ \left( \nu + \nu_t \right) \left( \frac{\partial u_j}{\partial x_i} \right) \right] \frac{\partial}{\partial x_j} \left[ \left( \nu + \nu_t \right) \left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i} \right) \right]
=
\frac{\partial}{\partial x_j} \left[ \left( \nu + \nu_t \right) \left( \frac{\partial u_i}{\partial x_j} \right) \right]
+
\frac{\partial}{\partial x_j} \left[ \left( \nu + \nu_t \right) \left( \frac{\partial u_j}{\partial x_i} \right) \right]](/Forums/vbLatex/img/97d79c0914c346e364d91d3eda5a9302-1.gif) The first term in the right-hand side is ok, by using Crank-Nicholson method. But the second term yielded a strong restriction in the CFL number. I tried both Adams-Bashforth and Crank-Nicheolson for the second term, but both of them needed very small dt. In the case I remove 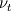 from the second term, it works fine, but including from the second term, it works fine, but including 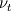 makes strong restrictions in time step. makes strong restrictions in time step. And my question: How can I remove this restriction from the second term? Is there any way? Thanks |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
Quote:
I don't understand your procedure...the eddy viscosity at time n+1 is unknown and the system would be not linear... |
|
|
|

|
|
|
|
|
#3 |
|
Member
M. Nabi
Join Date: Jun 2009
Posts: 44
Rep Power: 16  |
Right, it is unknown, but I iterate all momentum equations and the eddy viscosity (using Smagorinsky) until velocity field converges. Then use pressure correction equation, and correct the velocity field.
|
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
the terms in the RHS require (dt/2)* for the CN integration.
However, the restriction for the time step is very important, you need a small value |
|
|
|

|
|
|
|
|
#5 | |
|
Member
M. Nabi
Join Date: Jun 2009
Posts: 44
Rep Power: 16  |
Quote:
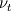 is few orders larger than is few orders larger than  , which makes the total viscosity large. The first term has no any problem as it is unconditionally stable by using CN. , which makes the total viscosity large. The first term has no any problem as it is unconditionally stable by using CN. In my case, the second term reduces the dt from 2e-3 to 1e-6 I wonder either there is a way to reduce the restriction for the second term. . I saw several papers use AB2-CN method with relatively large dt, but they didn't mention about the details. Thank you |
||
|
|

|
||
|
|
|
#6 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
the LINEAR stability analysi of the CN discretization leads to two eigenvalues from which one has stability unconditionally for one but not for the other. That means the coupling with the all terms of the equations leads to a stability region (cfl,Reh) with a strong restriction in the dt at low Reh.
Considering that you have a non linear case, the constraint on the dt is clearly strong. Actually, I am used to work by letting the CN scheme for the molecular viscous term and using explicit second order AB for the eddy viscosity term. |
|
|
|

|
|
|
|
|
#7 | |
|
Member
M. Nabi
Join Date: Jun 2009
Posts: 44
Rep Power: 16  |
Quote:
But using AB for eddy viscosity term, does it reduce the CFL restriction? Do you use also AB for the viscosity of the first term, or only for the second term? |
||
|
|

|
||
|
|
|
#8 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
First, the eddy viscosity can become locally high and the time scale needs to be small. Then, using an explicit AB scheme for the SGS term you avoid to work with a non-linear system having coefficents in the SGS terms.
|
|
|
|

|
|
|
|
|
#9 |
|
Member
M. Nabi
Join Date: Jun 2009
Posts: 44
Rep Power: 16  |
But how to avoid having coefficients in the SGS term? Even if it is explicit, still the eddy viscosity can be locally high from time step n, and it is included in SGS!!! Do you mean we have to linearize it by, for instance, Newton linearization?
|
|
|
|

|
|
|
|
|
#10 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
just using the explicit AB discretization requires eddy viscosity only at tn and tn-1, no coefficents are therefore present in the algebric system
|
|
|
|

|
|
|
|
|
#11 |
|
Member
M. Nabi
Join Date: Jun 2009
Posts: 44
Rep Power: 16  |
It is right, they will be known. But they will still restrict the CFL number as the value of eddy viscosity is large. Using explicit method such as AB2, lets the CFL number dependent on the size of cell quadratic, isn't it ?
|
|
|
|

|
|
|
|
|
#12 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
Quote:
the stability constraint is due to the combination of the type of time integration along with convective, diffusive and SGS terms. Generallly, the CFL must be quite smaller than 1 |
||
|
|

|
||
|
|
|
#13 | |
|
Member
M. Nabi
Join Date: Jun 2009
Posts: 44
Rep Power: 16  |
Quote:
Do you know any reference which explains the discretizations in details for LES? |
||
|
|

|
||
|
|
|
#14 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
if you want, some of my papers about discretization for LES are published on IJNMF. Details are provided for projection method with AB/CN discretization
|
|
|
|

|
|
|
|
|
#15 |
|
Member
M. Nabi
Join Date: Jun 2009
Posts: 44
Rep Power: 16  |
||
|
|

|
|
|
|
|
#16 |
|
Member
M. Nabi
Join Date: Jun 2009
Posts: 44
Rep Power: 16  |
||
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| How to determine time step size and Max. iterations per time step. | pratik c | FLUENT | 46 | January 21, 2024 12:21 |
| High Courant Number @ icoFoam | Artex85 | OpenFOAM Running, Solving & CFD | 11 | February 16, 2017 13:40 |
| Rapidly decreasing deltaT for interDyMFoam | chrisb2244 | OpenFOAM Running, Solving & CFD | 3 | July 1, 2014 16:40 |
| Micro Scale Pore, icoFoam | gooya_kabir | OpenFOAM Running, Solving & CFD | 2 | November 2, 2013 13:58 |
| number of iterations per time step | chouki | FLUENT | 1 | August 13, 2013 00:11 |